A useful reduction (SAT -> game) - PowerPoint PPT Presentation
Title:
A useful reduction (SAT -> game)
Description:
(Note as soon as one player plays default, the other player s best response is to also play default, leading to the Nash equilibrium at (default, default).) – PowerPoint PPT presentation
Number of Views:36
Avg rating:3.0/5.0
Title: A useful reduction (SAT -> game)
1
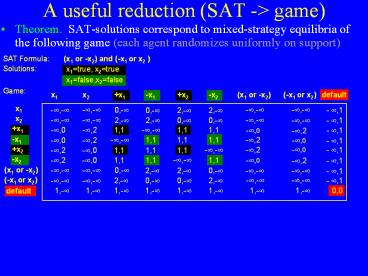
A useful reduction (SAT -gt game)
- Theorem. SAT-solutions correspond to
mixed-strategy equilibria of the following game
(each agent randomizes uniformly on support)
SAT Formula
(x1 or -x2) and (-x1 or x2 )
Solutions
x1true, x2true
x1false,x2false
Game
x1
x2
x1
-x1
x2
-x2
(x1 or -x2)
(-x1 or x2)
default
x1
-?,-?
0,-?
- ?,1
-?,-?
-?,-?
-?,-?
2,-?
2,-?
0,-?
x2
-?,-?
-?,-?
-?,-?
- ?,1
2,-?
2,-?
0,-?
0,-?
-?,-?
x1
-?,-?
-?,0
-?,2
1,1
1,1
1,1
- ?,1
-?,0
-?,2
-x1
-?,0
-?,2
1,1
1,1
1,1
-?,-?
-?,2
- ?,1
-?,0
x2
-?,-?
- ?,1
-?,2
-?,0
-?,2
-?,0
1,1
1,1
1,1
-x2
-?,-?
-?,2
-?,0
1,1
1,1
1,1
- ?,1
-?,2
-?,0
(x1 or -x2)
-?,-?
-?,-?
0,-?
-?,-?
-?,-?
- ?,1
2,-?
2,-?
0,-?
(-x1 or x2)
-?,-?
-?,-?
2,-?
-?,-?
-?,-?
- ?,1
2,-?
0,-?
0,-?
default
1,-?
1,-?
0,0
1,-?
1,-?
1,-?
1,-?
1,-?
1,-?
2
- Proof sketch
- Playing opposite literals (with any probability)
is unstable because the other player will
prefer to play a variable move . For example, if
the row player plays x1 then the column player
will play x2 which would prompt the first player
to change his/her move to default. (Note as soon
as one player plays default, the other players
best response is to also play default, leading to
the Nash equilibrium at (default, default).) - If you play literals (with probabilities), you
should make sure that - for any clause, the probability of the literal
being in that clause is high enough, and - for any variable, the probability that the
literal corresponds to that variable is high
enough - (otherwise the other player will play this
clause/variable and hurt you) - A player wont play any literal with a
probability greater than 1/n because the other
player will prefer to play a variable strategy
which has a large negative payoff for the first
player. For example if the row player plays x1
with a probability of 2/3 and x2 with a
probability of 1/3 then the column player would
be motivated to play x2 which is a big hit to the
row players payoff. - So equilibria where both randomize over literals
can only occur when both randomize over same SAT
solution - A player would not play a variable strategy
because the other player would play the default
strategy which results in a negative payoff for
the first player . The first player would then
decide to play the default move with a zero
payoff for both players. - Similarly for the clause stategies.
- The default move is needed because then it is
true that there is a satisfying assignment for
the SAT formula iff there is more than one mixed
Nash equilibrium in the game. To see why, note
that if there is no satisfying assignment, then
any mixed strategy that one of the players uses
would violate one of the clauses and would
motivate the other player to play a clause move
which leads to the default Nash the default Nash
is the only Nash and starting from any state, a
sequence of best replies will lead us there. If
there is a satisfying assignment, then not only
will (default,default) be a Nash, but the mixed
strategy profile where each player puts
probability 1/n on each literal of the satisfying
assignment will also be a Nash.
3
Complexity of mixed-strategy Nash equilibria with
certain properties
- This reduction implies that there is an
equilibrium where players get expected utility 1
each iff the SAT formula is satisfiable - Any reasonable objective would prefer such
equilibria to 0-payoff equilibrium - Corollary. Deciding whether a good equilibrium
exists is NP-hard - 1. equilibrium with high social welfare
- 2. Pareto-optimal equilibrium
- 3. equilibrium with high utility for a given
player i - 4. equilibrium with high minimal utility
- Also NP-hard (from the same reduction)
- 5. Does more than one equilibrium exists?
- 6. Is a given strategy ever played in any
equilibrium? - 7. Is there an equilibrium where a given strategy
is never played? - (5) weaker versions of (4), (6), (7) were known
Gilboa, Zemel GEB-89 - All these hold even for symmetric, 2-player games
4
Counting the number of mixed-strategy Nash
equilibria
- Why count equilibria?
- If we cannot even count the equilibria, there is
little hope of getting a good overview of the
overall strategic structure of the game - Unfortunately, our reduction implies
- Corollary. Counting Nash equilibria is P-hard!
- Proof. SAT is P-hard, and the number of
equilibria is 1 SAT - Corollary. Counting connected sets of equilibria
is just as hard - Proof. In our game, each equilibrium is alone in
its connected set - These results hold even for symmetric, 2-player
games