Figure%209-1 - PowerPoint PPT Presentation
Title:
Figure%209-1
Description:
Heaps The heap is guaranteed to hold the largest node of the tree in the root. The smaller nodes of a heap can be placed on eighter the left or right – PowerPoint PPT presentation
Number of Views:50
Avg rating:3.0/5.0
Title: Figure%209-1
1
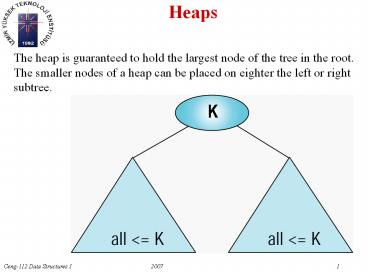
Heaps
The heap is guaranteed to hold the largest node
of the tree in the root. The smaller nodes of a
heap can be placed on eighter the left or
right subtree.
Figure 9-1
2
Heaps
- A heap is a binary tree structure with the
following rules - The tree is complete or nearly complete.
- The key value of each node is greater than or
equal to the key value of each of its
descendents. - They are often implemented in an array rather
than a linked list. We are able to calculate the
location of the right and left subtrees.
3
Heaps
Figure 9-2
4
Heaps
Figure 9-3
5
Figure 9-8
6
Heap Data Structure
- A heap can be built in a dynamic tree structure.
It is most often implemented in an array. This
implementation is possible, because the heap is
complete or nearly complete. Therefore the
relationship between a node and its children is
fixed and can be calculated as shown below
7
Heap Data Structure
- For a node located at index i,
- its children are found at
- Left child 2i 1
- Right child 2i 2
- its parent is located at (i 1)/2
- Given the index for a left child j
- its right sibling (j 1)
- Given the index for a right child k
- its left sibling (k 1)
- Given the size n of a complete heap, the location
of the first leaf is n/2.
8
Basic Heap Algorithms
- There are two basic maintenance operations that
are performed on a heap - Insert a node and,
- Delete a node.
- To implement the insert and delete operations, we
need two basic algorithms - reheap up
- reheap down
9
Heap Algorithms - ReheapUp
Figure 9-4
10
Figure 9-5
11
Heap Algorithms - ReheapUp
- algorithm reheapUp (ref heap ltarraygt, val
newnode ltindexgt) - Reestablishes heap by moving data in child up to
its correct location in the heap array. - PRE heap is array containing an invalid heap.
- newNode is index location to new data in
heap. - POST newNode has been inserted into heap.
- 1 if (newNode not zero)
- 1 parent (newNode 1) / 2
- 2 if (heapnewNode.key gt heapparent.key)
- 1 swap(newNode, parent)
- 2 reheapup(heap, parent)
- 2 return
- end reheapUp
12
Heap Algorithms - ReheapDown
Figure 9-6
13
(No Transcript)
14
Heap Algorithms - ReheapDown
- algorithm reheapDown (ref heap ltarraygt, val root
ltindexgt, val last ltindexgt) - Reestablishes heap by moving data in root down to
its correct location in the heap array. - PRE heap is an array data.
- root is root of heap or subheap.
- last is an index to the last element in heap.
- POST heap has been restored.
15
Heap Algorithms - ReheapDown
- algorithm reheapDown (ref heap ltarraygt, val root
ltindexgt, - val last ltindexgt)
- Determine which child has larger key.
- 1 if (root 2 1 lt last)
- There is at least one child.
- 1 leftKey heaproot 2 1.data.key
- 2 rightkey heaproot 2 2.data.key
- 3 if (leftKey gt rightKey)
- 1 largeChildKey leftKey
- 2 largeChildIndex root 2 1
- 4 else
- 1 largeChildKey rightKey
- 2 largeChildIndex root 2 2
- Test if root gt larger subtree.
- 5 if (heaproot.data.key lt heaplargeChildIndex
.data.key) - 1 swap(root, largeChildIndex)
- 2 reheapDown(heap, largeChildIndex, last)
- end reheapdown
16
Heap Algorithms - Build Heap
wall
The build heap algorithm is very simple. Given
the array we need to convert to a heap, we walk
through the array, starting at the second
element, calling reheap up for each array element
to be inserted into the heap. algorithm
buildHeap(ref heap ltarraygt, val size
ltintegergt) 1 walker 1 2 loop (walker lt size)
1 reheapUp(heap, walker) 2 walker
walker 1 3 return end buildHeap
17
Heap Algorithms - Insert Heap
- To insert a node we need to locate the
- first empty leaf in the array.
- We move the new data to the first empty
- leaf and reheap up.
- algorithm insertHeap(ref heap ltarray of
dataTypegt, - ref last ltindexgt,
- ref data ltdataTypegt)
- 1 if (heap full)
- 1 return false
- 2 lastlast 1
- 3 heaplast data
- 4 reheapUp (heap, last)
- 5 return true
- end insertHeap
Figure 9-10
18
Heap Algorithms - Delete Heap
algorithm deleteHeap(ref heap ltarray of
dataTypegt, ref last ltindexgt, ref
dataOut ltdataTypegt) Deletes root of heap and
passes data back to caller. Root has been deleted
from heap and root data placed in
dataOut. 1 if (heap empty) 1 return false 2
dataOut heap0 3 heap0 heaplast 4 last
last - 1 5 reheapDown (heap, 0, last) 6 return
true end deleteHeap
Figure 9-11
19
Heap Applications
- Common applications of Heaps are
- Selection algorithms,
- Priority queues,
- Sorting.
20
Heap Applications Selection Algorithms
- To determine the kth element in an unsorted list,
there are two solution - First sort the list and select the element at
location k, or - Create a heap and delete k-1 elements from it.
21
Heap Applications Selection Algorithms
Example If we want to know the fourth largest
element of the list
Figure 9-12
22
Heap Applications Priority Queues
- The heap is an excellent structure to use for a
priority queue. - One common technique uses an encoded priority
number that consists of the priority plus a
sequential number represents the events place
within the queue. The serial number must be in
descending order.
23
Heap Applications Priority Queues
Figure 9-13
24
Exercise
Which of the structures is a heap and which is
not?
Figure 9-15
25
Exercise
Apply the reheapUp algorithm to this nonheap
structure
Figure 9-16
26
Exercise
Apply the reheapDown algorithm to this nonheap
structure
Figure 9-17
27
Exercise
- Show the array implementation.
- Apply the delete operation. Repair the heap after
the deletion. - Insert 38 in the heap. Repair the heap after the
insertion.
Figure 9-18
28
Exercise
- Show the left and right children of 32 and 27 in
the heap. - Show the left children of 14 and 40.
- Show the parent of 11, parent of 20 and parent of
25.
Figure 9-19
29
Exercise
- Which of the following sequences are heaps?
- 42 35 37 20 14 18 7 10
- 42 35 18 20 14 30 10
- 20 20 20 20 20 20
30
HW-10
- Use array structure and create a Heap tree with
positive integer numbers which are taken from the
screen. - Array should include 14 data entry.
- Collect firts 8 entries from the user in this
array as unordered. - Use buildheap algorithm and establish the heap
tree structure on this array - Collect the other entries from user with add new
node option and use insertheap algortihm to
placed the node in correct position. - Write the Heep delete function which establishes
to delete root entry from the Heap. - Write a function which lists the entries of the
Heap in array structure. - Collect all above functions under a user menu.
Load your HW-10 to FTP site until 21 May. 07 at
0900 am.