Hash Tables - PowerPoint PPT Presentation
1 / 16
Title:
Hash Tables
Description:
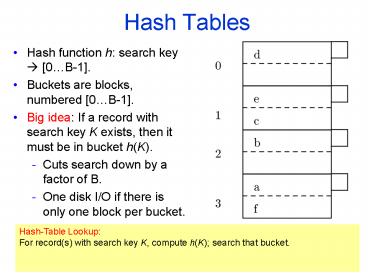
Hash Tables Hash function h: search key [0 B-1]. Buckets are blocks, numbered [0 B-1]. Big idea: If a record with search key K exists, then it must be in bucket h(K). – PowerPoint PPT presentation
Number of Views:152
Avg rating:3.0/5.0
Title: Hash Tables
1
Hash Tables
- Hash function h search key ? 0B-1.
- Buckets are blocks, numbered 0B-1.
- Big idea If a record with search key K exists,
then it must be in bucket h(K). - Cuts search down by a factor of B.
- One disk I/O if there is only one block per
bucket.
HashTable Lookup For record(s) with search key
K, compute h(K) search that bucket.
2
HashTable Insertion
- Put in bucket h(K) if it fits otherwise create
an overflow block. - Overflow block(s) are part of bucket. Example
Insert record with search key g.
3
What if the File Grows too Large?
- Efficiency is highest if
- records lt buckets ? (records/block)
- If file grows, we need a dynamic hashing method
to maintain the above relationship. - Extensible Hashing double the number of buckets
when needed. - Linear hashing add one more bucket as
appropriate.
4
Dynamic Hashing Framework
- Hash function h produces a sequence of k bits.
- Only some of the bits are used at any time to
determine placement of keys in buckets. - Extensible Hashing (Buckets may share blocks!)
- Keep parameter i number of bits from the
beginning of h(K) that determine the bucket. - Bucket array now pointers to buckets.
- A block can serve as several buckets.
- For each block, a parameter j?i tells how many
bits of h(K) determine membership in the block. - I.e., a block represents 2i-j buckets that share
the first j bits of their number.
5
Example
- An extensible hash table when i1
6
Extensible Hashtable Insert
- If record with key K fits in the block pointed to
by h(K), put it there. - If not, let this block B represent j bits.
- jlti
- Split block B into two and distribute the records
(of B) according to (j1)st bit - set jj1
- fix pointers in bucket array, so that entries
that formerly pointed to B now point either to B
or the new block - How?
- depending on(j1)st bit
- ji
- Set ii1
- Double the bucket array, so it has now 2i1
entries - proceed as in (1).
Let w be an old array entry. Both the new
entries w0 and w1 point to the same block that w
used to point to.
7
Example
- Insert record with h(K) 1010.
8
Example Next
- Next records with h(K)0000 h(K)0111.
- Bucket for 0... gets split,
- but i stays at 2.
- Then record with h(K) 1000.
- Overflows bucket for 10...
- Raise i to 3.
9
Extensible Hash Tables
- Advantages
- Lookup never search more than one data block.
- Hope that the bucket array fits in main memory
- Defects
- Substantial amount of work to double the bucket
array - Interrupts access to data file
- Makes certain insertions appear to take very long
- Doubling the bucket array soon is going to make
the array to not fit in main memory. - Problem with skewed key distributions.
- E.g. Let 1 block2 records. Suppose that three
records have hash values, which happen to be the
same in the first 20 bits. - In that case we would have i20 and and one
million bucket-array entries, even though we have
only 3 records!!
10
Linear Hashing
- Use i bits from right (loworder) end of h(K).
- Buckets numbered 0n-1, where 2i-1ltn?2i.
- Let last i bits of h(K) be m (a1,a2,,ai)
- If m lt n, then record belongs in bucket m.
- If n?mlt2i, then record belongs in bucket m-2i-1,
that is the bucket we would get if we changed a1
(which must be 1) to 0.
i1
n2
r3
of buckets
of records
This is also part of the structure
11
Linear HashTable Insert
- Pick an upper limit on capacity,
- e.g., 85 (1.7 records/bucket in our example).
- If an insertion exceeds capacity limit, set n
n 1. - If new n is 2i 1, set i i 1. No change in
bucket numbers needed --- just imagine a leading
0. - Need to split bucket n - 2i-1 because there is
now a bucket numbered (old) n.
12
Example
- Insert record with h(K) 0101.
- Capacity limit exceeded increment n.
13
Example
- Insert record with h(K) 0001.
- Capacity limit not exceeded.
- But bucket is full add overflow bucket.
i2
n3
r5
14
Example
- Insert record with h(K) 1100.
- Capacity exceeded set n 4, add bucket 11.
- Split bucket 01.
15
Lookup in Linear Hash Table
- For record(s) with search key K, compute h(K)
search the corresponding bucket according to the
procedure described for insertion. - If the record we wish to look up isnt there, it
cant be anywhere else. - E.g. lookup for a key which hashes to 1010, and
then for a key which hashes to 1011.
i2
n3
r4
16
Exercise
- Suppose we want to insert keys with hash values
00001111 in a linear hash table with 100
capacity threshold. - Assume that a block can hold three records.