ADHD Reaction Times: Densities, Mixed Effects, and PCA

1
ADHD Reaction TimesDensities, Mixed Effects,
and PCA
2
ADHD Attention Deficit (Hyperactive) Disorder

• ADHD kids have difficulty in focusing on tasks.
• But true ADHD is rarer than is generally
  believed, and drug treatments are used much too
  often.
• How can we correctly identify ADHD children?

3
Reaction Time Experiment

• 17 ADHD children
• 16 age-matched controls
• Warning of cue appears on computer screen.
• Delay of about 10 seconds.
• Cue actually appears.
• Measure the time it takes to react to the cue.
• Repeat and get about 70 reaction times for each
  child.
• Longer reaction times for ADHD than for controls.
  But what do they look like? How to quantify?

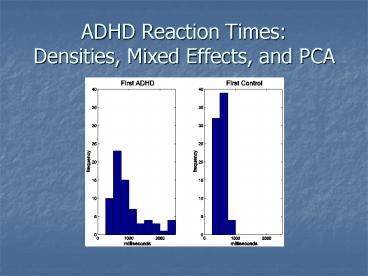
4
How do reaction times differ between ADHD and
controls?

• ADHD child has many reaction times beyond 1 sec.
  Not so for control.
• How can we represent histogram as a smooth
  density?
• What are differences in shape, mean, mode, etc.,
  between groups?
• How can we account for child-to-child differences
  when comparing the groups?

5
How can we represent the histogram as a smooth
curve?

• Simple answer Find the probability density
  function using standard methods.
• Problem with that Standard textbook densities
  dont capture characteristics like
• Initial lag
• Extreme peak immediately after lag
• Long right tail with many outliers
• New answer Use flexible modeling of density
  functions to create a functional data object

6
How can we create a functional density object
from a histogram?

• Use tools from before
• Basis expansion linear combination of splines
• Roughness Penalty making explicit the competing
  goals
• Basis expansion with
• 34 B-splines of order 5
• Equally spaced knots
• Competing goals are
• Fitting density curve exactly to histogram
• Wanting curve to be close to a normal density

7
What about the constraints of a probability
density function?

• Constraints
• P(t) gt 0 over interval of interest.
• Area under the curve is 1.
• New tool Transformation.
• For any function W(t), can build a density
  function
• p(t) C expW(t), for C appropriate function
  of W.
• Transforms estimation problem from constrained
  p(t) to unconstrained W(t)!

8
Hey, the original data arent really functional,
are they?

• Idea again Transformation.
• The functional object is really indirectly
  related to the data.
• Data reaction times t nonfunctional
• What we want reaction time densities p(t)
  functional
• Related through

9
What do the group densities look like?

• Definite shift in mode between groups.
• Bimodality, or even trimodality?
• ADHD has large shoulder and long tail.
• But what about individual differences in children?

10
Are there inter-child differences?

• Examples of four ADHD children
• Dashed line is group density for ADHD.
• Solid line is individual density for child.
• Definite child-to-child variability. Shouldnt
  ignore this.

11
How can we estimate the densities and account for
individual differences?
Functional Mixed Effects Linear Model

• Transform first
• Subtract 120 from each reaction time
• Initial dead period not helpful
• Logarithm
• Effects are likely multiplicative, not additive
• Z log10(t-120)

12
What is our functional mixed effects model?

• Build mixed effects model
• Child i trial j group k
• Zijk transformed reaction time density
  (functional)
• µk typical performance of all children in group
  k (functional)
• aik individual performance of child i within
  group k (functional)
• Uijk leftover variation in density (functional)

Zijk µk a ik Uijk ? aik 0
13

• ADHD have greater variability in residuals.
• ADHD have greater mean residuals (952 vs 645
  msec).
• Modality an artifact of instruments.

14
How can we explore variability across subjects
within a group?
Functional Principal Components Analysis

• Goal
• explore how densities change from child to child.
• Idea
• Principal components (harmonics) are like
  empirical basis functions. Want to expand our
  densities with these harmonics.
• Problem
• Hard to ensure that the densities are positive.
• Solution
• Transformation! Explore the derivatives instead.
  

15
What do the harmonics look like?

• Used weighted fPCA
• minimizes importance of variation when density is
  small.
• Back-transformed
• to get harmonics in original density scale.
• Harmonic Interpretations
• 1st More weight on central peak.
• 2nd More weight on early reaction times.
• 3rd Highlights periodic effect from
  instrumentation.

16
What have we learned?

• Transformations
• The functional object can be indirectly related
  to the data, such as the probability density
  function
• Functional Linear Model
• Can add random effects
• Functional Principal Components Analysis
• Can be done on a transformation, such as the log
  density derivative