Functions

1
Functions

• Lecture 12

2
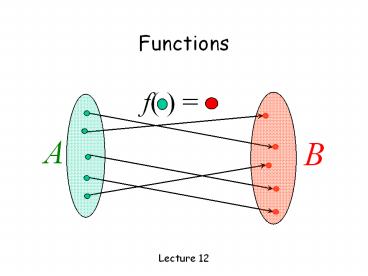
Functions
function, f, from set A to set B associates an
element , with an element
The domain of f is A. The codomain of f is B.
For every input there is exactly one output.
3
Functions
4
Functions
f(S) S
f(string) length(string)
f(student) student-ID
f(x) is-prime(x)
5
Injections (one-to-one)
is an injection iff every element of B is f of
at most 1 thing
1 arrow in
A B
6
Surjections (Onto)
is a surjection iff every element of B is f of
something
?1 arrow in
A
B
A B
7
Bijections
is a bijection iff it is surjection and injection.
exactly one arrow in
A B
8
Functions

• a. One-to-one, b. Onto, c. One-to-one, d.
  neither d. Not a
• Not onto not one-to-one and
  onto function
• a 1 a a 1 a 1 1
• b 2 b 1 b 2 b 2 a 2
• c 3 c 2 c 3 c 3 b 3
• 4 d 3 d 4 d 4 c 4

8
9
In-Class Exercises
Function Domain Codomain Injective? Subjective? Bijective?
f(x)sin(x) Real Real
f(x)2x Real Positive real
f(x)x2 Real Positive real
Reverse string Bit strings of length n Bit strings of length n
10
Inverse Sets
A
B
Given an element y in B, the inverse set of y
f-1(y) x in A f(x) y.
11
Inverse Function
Informally, an inverse function f-1 is to undo
the operation of function f.
exactly one arrow in
There is an inverse function f-1 for f if and
only if f is a bijection.
12
Composition of Functions
Two functions fX-gtY, gY-gtZ so that Y is a
subset of Y, then the composition of f and g is
the function g?f X-gtZ, where g?f(x) g(f(x)).
Y
Z
X
Y
13
In-Class Exercises
Function f Function g Injective? Subjective? Bijective?
fX-gtY f subjective gY-gtZ g injective
fX-gtY f subjective gY-gtZ g subjective
fX-gtY f injective gY-gtZ g subjective
fX-gtY f bijective gY-gtZ g bijective
fX-gtY F-1Y-gtX