R - PowerPoint PPT Presentation
Title: R
1
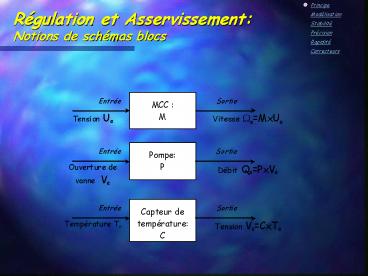
Régulation et AsservissementNotions de schémas
blocs
2
Régulation et AsservissementNotions de schémas
blocs
- Comparateur ou sommateur
3
Régulation et AsservissementNotions de schémas
blocs
4
Régulation et AsservissementNotions de schémas
blocs
5
Régulation et AsservissementNotions de schémas
blocs
Transmittance en boucle fermée
6
Régulation et AsservissementNécessité de réguler
7
Régulation et AsservissementBoucle ouverte
Organes de commande dun four
8
Régulation et AsservissementBoucle fermée
Organes de commande dun four
9
Régulation et AsservissementEléments
constitutifs
un capteur une consigne (fixe ou variable
dans le temps) un comparateur délivrant un
signal décart une loi de commande qui
calcule le signal à envoyer sur lactionneur
un actionneur le système physique à commander
et soumis à des perturbations.
PID
10
Les critères dun asservissement
- améliorer la rapidité de fonctionnement du
système - augmenter la précision
- diminuer linfluence des perturbations
- rendre contrôlable un système qui ne lest pas
en boucle ouverte - diminuer les effets non linéaires des processus
Précision
Rapidité
Stabilité
BON
MAUVAIS
11
Les correcteurs
Afin daméliorer la régulation les correcteurs
sont de trois types
12
Création dune régulation
- Quelle grandeur on veut maitriser?
- Quelle mesure est faite sur le système?
- Sur quel actionneur agit-on?
- Sassurer que le comparateur mesure bien une
erreur par rapport à la consigne. - Amplifier lerreur correcteur KP ou bande
proportionnelle - Affinage de la stratégie de régulation
- Stratégie doptimisation à tâtons
- Stratégies doptimisation Identification de la
boucle puis Strejc, Broida, Ziegler Nichols - Stratégie doptimisation auto apprentissage de
certains régulateurs
13
Carte heuristique
14
Modélisation des systèmes linéaires
15
Modélisation des systèmes linéaires
- On étudie la réponse temporelle à un échelon de
tension ( méthode indicielle ). - La tension de commande varie sinusoïdalement on
détermine la transmittance complexe du système
amplification et déphasage pour une fréquence
donnée
- Cette dernière étude donne lieu à divers type de
représentation - Bode
- Nyquist
- Black
16
Bode - Nyquist - Black
- Bode
- En ordonnées 20 log (T) et Arg (T)
- En abscisse la fréquence sur une échelle log(f)
- Nyquist courbe paramétrée en f
- en ordonnée ?m(T)
- en abscisses ?é(T)
- Black courbe paramétrée en f
- en ordonnée 20 log (T)
- en abscisses Arg (T)
17
Modélisation des systèmes linéaires
Modèle du premier ordre
18
Modélisation des systèmes linéaires
Modèle du second ordre
19
Modélisation des systèmes linéaires
Modèle de Broïda
20
Modélisation des systèmes linéaires
Modèle de Strejc
21
Transmittance d'un système asservi
- Transmittance en boucle ouverte
Transmittance en boucle fermée
22
Stabilité d'un système asservi
Condition de stabilité
- Un système est stable si sa fonction de transfert
- ne comporte que des pôles (valeurs de p annulant
) à partie réelle strictement
négative . - En effet, loriginale dune fraction à pôle dont
la partie réelle est négative est une
exponentielle décroissante - dans le cas dun pôle réel négatif
- dans le cas de pôles
complexes conjugués à partie réelle négative
23
Critères de stabilité
- Sur un système modélisé ainsi
La recherche des pôles de F(p) conduit à étudier
24
Critères de stabilité
- Critères mathématiques
- Critère de Routh-Hurwitz
- Critère du lieu des racines
- Critère graphiques
- Critère de Nyquist
- Critère de Black-Nichols
- Critère dans le diagramme de Bode
25
Critère de Routh-Hurwitz
- Aucun des ?i nest nul
- Tous les ?i sont de même signe
- Après construction du tableau suivant les
coefficients de la première colonne sont de même
signes
26
Critère du lieu des racines
- http//eig.unige.ch/allenbach/Thummel/index.html
27
Critère de Nyquist
Toutes les racines de ont une partie réelle
strictement négative (système stable) si le
diagramme de Nyquist de la B.O. nentoure pas le
point -1
Critère du Revers
Le système est stable en boucle fermée si le
diagramme de Nyquist de la transmittance en B.O.
laisse le point 1 sur sa gauche lorsque la
pulsation ? varie de 0 à linfini.
28
Critère de Black Nichols
- Si on laisse le point critique à sa droite quand
on décrit la courbe de T(j?) dans le sens des ?
croissants le système est stable.
29
Critères dans le diagramme de Bode
- Pour la fréquence ?u pour laquelle TdB (?u) 0 si
- ?(?u )gt-? stable
- ?(?u )lt-? instable
OU
- Pour la fréquence ?C pour laquelle Arg(T)-? si
- T(?C )gt1 instable
- T(?c )lt1 stable
30
Marges de Gain et de Phase
Marge de phase (sur la boucle ouverte) Déphasage
supplémentaire qui ferait passer la courbe de
lautre côté du point critique. Valeur dont il
faut augmenter ? pour KH 1 pour arriver au point
critique ?En pratique . Marge de gain (sur la
boucle ouverte) Nombre de dB dont on peut
augmenter le gain sans provoquer
linstabilité. Valeur dont il faut augmenter KH
lorsque ? -180 pour arriver au point critique ?
En pratique
31
Précision
- Un système est précis si la sortie suit l'entrée
quelles que soient les circonstances. L'écart est
la différence entre la valeur souhaitée et la
valeur obtenue
Lerreur est définie par
soit en se servant du théorème de la valeur
finale
32
Précision
- Or la FTBO est caractérisée par sa classe
dintégration qui est la puissance ? définie ci
dessous
33
Critère de Rapidité dun système
- Obtention du meilleur temps de réponse tr5 (voir
exercice chauffage) - Obtention du meilleur temps de réponse critères
(AIE minimisation de lintégrale de lerreur)
34
Correcteurs
- Correcteur proportionnel
35
Correcteurs
- Correcteur intégral
Il joue sur la précision en éliminant lerreur en
régime permanent (élimine lerreur statique )
Plus laction intégrale est élevée (Ti petit),
plus la réponse saccélère et plus la stabilité
se dégrade
36
Correcteurs
- Correcteur dérivé
Laction Dérivée améliore la stabilité et
donne un coup de pied au système.
37
(No Transcript)
38
Correcteurs
- Diverses structures
- Parallèle
- Série
- Mixte
39
Correcteurs
- Choix
En Boucle Ouverte (Broïda il est cependant rare
que lon puisse faire des essais en BO)
En Boucle Fermée (Ziegler Nichols ou méthode de
lultime pompage).