Definition

1
Definition
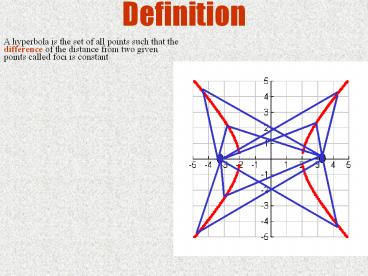
A hyperbola is the set of all points such that
the difference of the distance from two given
points called foci is constant
2
Definition
The parts of a hyperbola are
transverse axis
3
Definition
The parts of a hyperbola are
conjugate axis
4
Definition
The parts of a hyperbola are
center
5
Definition
The parts of a hyperbola are
vertices
6
Definition
The parts of a hyperbola are
foci
7
(No Transcript)
8
(No Transcript)
9
(No Transcript)
10
(No Transcript)
11
(No Transcript)
12
Definition
The parts of a hyperbola are
the asymptotes
13
Definition
The distance from the center to each vertex is a
units
a
14
Definition
The distance from the center to the rectangle
along the conjugate axis is b units
b
15
Definition
The distance from the center to each focus is c
units where
c
16
Sketch the graph of the hyperbolaWhat are the
coordinates of the foci?What are the coordinates
of the vertices?What are the equations of the
asymptotes?
17
(No Transcript)
18
How do get the hyperbola into an up-down
position?
switch x and y
identify vertices, foci, asymptotes for
19
(No Transcript)
20
Definition
Standard equations
where (h,k) is the center
21
Definition
The equations of the asymptotes are
for a hyperbola that opens left right
22
Definition
The equations of the asymptotes are
for a hyperbola that opens up down
23
Summary

• Vertices and foci are always on the transverse
  axis

• Distance from the center to each vertex is a units

24
Summary

• If x term is positive, hyperbola opens left
  right

• If y term is positive, hyperbola opens up down

• a2 is always the positive denominator

25
Example
Find the coordinates of the center, foci, and
vertices, and the equations of the asymptotes for
the graph of
then graph the hyperbola.
Hint re-write in standard form
26
Solution
Center (-3,2) Foci (-3 ,2)
Vertices (-2,2), (-4,2)
Asymptotes
27
Example
Find the coordinates of the center, foci, and
vertices, and the equations of the asymptotes for
the graph of
then graph the hyperbola.
28
Solution
Center (-4,2) Foci (-4,2 )
Vertices (-4,-1), (-4,5)
Asymptotes