Raw H2RG Image

1
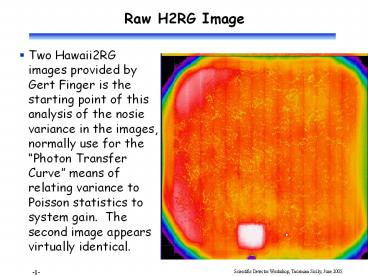
Raw H2RG Image

• Two Hawaii2RG images provided by Gert Finger is
  the starting point of this analysis of the nosie
  variance in the images, normally use for the
  Photon Transfer Curve means of relating
  variance to Poisson statistics to system gain.
  The second image appears virtually identical.

2
Difference H2RG image

• The difference of these two images still shows
  structure, but much of it has disappeared. Note
  the vertical stripes which will appear
  prominently in the power spectrum.

3
Central 1024 Difference

• Choosing the central 1024x1024 pixels in
  preparation for Fourier transforming the
  difference.
• Again, note not only the wide-spaced vertial
  stripes, but the closely spaced stripes.

4
Power Spectrum

• The power spectrum of the difference shows noise
  which has obvious power features
• Horizontal line vertical stripes
• Spots closely spaced vertical stripes
• Central spot various large-scale features
  remaining in difference

5
Binned Power Spectrum

• Binning the power spectrum 8x8 and increasing the
  stretch makes non-uniformity in the power
  spectrum more obvious.
• The power at the Nyquist frequency (corners) is
  significantly smaller than the asymptote as k -gt
  0.
• The Poisson variance from the photons impinging
  on the detector has been suppressed by
  convolution with some sort of pixel-to-pixel
  correlation. The best estimate of the
  pre-convolution is the k-gt0 asymptote.
• There is also significant non-circular uniformity
  apparent, indicating that the convolution is
  worse in the horizontal direction than the
  vertical direction.

6
Masked for Averaging

• To make a quantitative estimate of the error in
  variance estimation, mask out the features which
  are obviously caused by large scale detector
  characteristics rather than pixel-to-pixel
  correlations.

7
Azimuthal Average

• Despite the fact that the power spectrum is not
  accurately circular, take an azimuthal average so
  that we can examine the power spectrum as a
  function of k.

8
Power Spectrum as a function of k

• Take a cut through the azimuthal average to show
  the variance as a function of wavenumber.
• The big peak at k0 is large-scale structure
  which is caused by detector non-uniformities.
• K63 is the Nyquist frequency and the direct
  pixel-to-pixel correlation.
• The big challenge is to understand what variance
  comes from pixel-to-pixel variations and what
  comes from large scale structure. We have used
  differencing to suppress the latter, but it is
  not perfect.

9
Ln Power Spectrum and k2 Fit

• As a naïve starting point, imagine that the
  pixel-to-pixel correlation has a Gaussian form.
  If so we can fit the natural log of the power
  with a parabola.
• This has a reasonable match to high k, but
  obviously does not explain low k large-scale
  features.

10
Ln Power Spectrum and k4 Fit
11
Ln Power Spectrum and k4 Fit

• A more likely pixel-to-pixel correlation arises
  from mutual capacitance, which might vary as r-3.
  I dont recall the 2-D Fourier tranform of this,
  but a Lorenzian FTs to an exponential, so we
  might expect that ln power should go linearly
  with k. Fitting a quartic polynomial
  demonstrates another division of power between
  pixel-to-pixel variance and large scale detector
  structure.
• Quantitatively, the difference between Nyquist
  and k0 is an offset in logarithm of 0.20, which
  means that a gain determined by variance over
  signal will be underestimated by a factor of
  1.22.