Binary Trees - PowerPoint PPT Presentation
Title:
Binary Trees
Description:
Binary Trees A binary tree is made up of a finite set of nodes that is either empty or consists of a node called the root together with two binary trees called the ... – PowerPoint PPT presentation
Number of Views:87
Avg rating:3.0/5.0
Title: Binary Trees
1
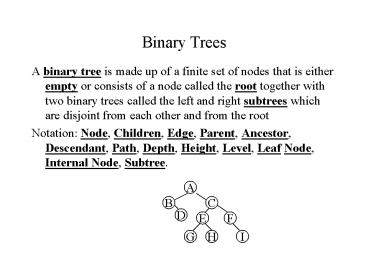
Binary Trees
- A binary tree is made up of a finite set of nodes
that is either empty or consists of a node called
the root together with two binary trees called
the left and right subtrees which are disjoint
from each other and from the root - Notation Node, Children, Edge, Parent, Ancestor,
Descendant, Path, Depth, Height, Level, Leaf
Node, Internal Node, Subtree.
A
C
B
D
F
E
G
I
H
2
Full and Complete Binary Trees
- A Full binary tree has each node being either a
leaf or internal node with exactly two non-empty
children. - A Complete binary tree If the height of the tree
is d, then all levels except possibly level d are
completely full. The bottom level has all nodes
to the left side.
3
Full Binary Tree Theorem
- Theorem The number of leaves in a non-empty full
binary tree is one more than the number of
internal nodes. - Proof (by Mathematical Induction)
- Base Case A full binary tree with 1 internal
node must have two leaf nodes. - Induction Hypothesis Assume any full binary tree
T containing n-1 internal nodes has n leaves. - Induction Step Pick an arbitrary leaf node j of
T. Make j an internal node by giving it two
children. The number of internal nodes has now
gone up by 1 to reach n. The number of leaves
has also gone up by 1. - Corollary The number of NULL pointers in a
non-empty binary tee is one more than the number
of nodes in the tree.
4
Traversals
- Any process for visiting the nodes in some order
is called a traversal. - Any traversal that lists every node in the tree
exactly once is called an enumeration of the
trees nodes. - Preorder traversal Visit each node before
visiting its children. - Postorder traversal Visit each node after
visiting its children. - Inorder traversal Visit the left subtree, then
the node, then the right subtree. - void preorder(BinNode root)
- if (rootNULL) return
- visit(root)
- preorder(root-gtleftchild())
- preorder(root-gtrightchild())
5
Expression Trees
- Example of (a-b)/((xy3)-(6z))
/
-
-
a
b
6
z
3
y
x
6
Binary Search Trees
- Left means less right means greater.
- Find
- If itemltcur-gtdat then curcur-gtleft
- Else if itemgtcur-gtdat then curcur-gtright
- Else found
- Repeat while not found and cur not NULL
- No need for recursion.
7
Find min and max
- The min will be all the way to the left
- While cur-gtleft ! NULL, curcur-gtleft
- The max will be all the way to the right
- While cur-gtright !NULL, curcur-gtright
- Insert
- Like a find, but stop when you would go to a null
and insert there.
8
Remove
- If node to be deleted is a leaf (no children),
can remove it and adjust the parent node (must
keep track of previous) - If the node to be deleted has one child, remove
it and have the parent point to that child. - If the node to be deleted has 2 children
- Replace the data value with the smallest value in
the right subtree - Delete the smallest value in the right subtree
(it will have no left child, so a trivial delete.
9
Array Implementation
- For a complete binary tree
- Parent(x)
- Leftchild(x)
- Rightchild(x)
- Leftsibling(x)
- Rightsibling(x)
(x-1)/2
2x1
2x2
x-1
x1
10
Huffman Coding Trees
- Each character has exactly 8 bits
- Goal to have a message/file take less space
- Allow some characters to have shorter bit
patterns, but some characters can have longer. - Will not have any benefit if each character
appears with equal probability. - English does not have equal distribution of
character occurance. - If we let the single bit 1 represent the letter
E, then no other character can start with a 1.
So some will have to be longer.
11
The Tree
- Look at the left pointer as the way to go for a 0
and the right pointer is the way to go for a 1. - Take input string of 1s and 0s and follow them
until hit null pointer, then the character in
that node is the character being held. - Example
- 0 E
- 10 T
- 110 P
- 111 F
- 0110111010EPFET
E
T
F
P
12
Weighted Tree
- Each time we have to go to another level, takes
time. Want to go down as few times as needed. - Have the most frequently used items at the top,
least frequently items at the bottom. - If we have weights or frequencies of nodes, then
we want a tree with minimal external path weight.
13
Huffman Example
- Assume the following characters with their
relative frequencies. - Z K F C U D L E
- 2 7 24 32 37 42 42 120
- Arrange from smallest to largest.
- Combine 2 smallest with a parent node with the
sum of the 2 frequencies. - Replace the 2 values with the sum. Combine the
nodes with the 2 smallest values until only one
node left.
14
Huffman Tree Construction
- Z K F C U D L E
- 2 7 24 32 37 42 42 120
306
186
120 E
79
107
65
37 U
42 D
42 L
33
32 C
9
24 F
2 Z
7 K
15
Results
- Let Freq Code Bits Mess. Len. Old Bits Old Mess.
Len. - C 32 1110 4 128 3 96
- D 42 101 3 126 3 126
- E 120 0 1 120 3 360
- F 24 11111 5 120 3 72
- K 7 111101 6 42 3 21
- L 42 110 3 126 3 126
- U 37 100 3 111 3 111
- Z 2 111100 6 12 3 6
- TOTAL 785 918
16
Heap
- Is a complete binary tree with the heap property
- min-heap All values are less than the child
values. - Max-heap all values are greater than the child
values. - The values in a heap are partially ordered.
There is a relationship between a nodes value
and the value of its children nodes. - Representation Usually the array based complete
binary tree representation.
17
Building the Heap
- Several ways to build the heap. As we add each
node, or create a tree as we get all the data
and then heapify it. - More efficient if we wait until all data is in.
1
1
2
3
5
7
4
5
6
7
4
2
6
3
7
7
5
1
5
6
4
2
6
3
4
2
1
3
18
Heap ADT
- class heap
- private
- ELEM Heap
- int size
- int n
- void siftdown(int)
- public
- heap(ELEM, int, int)
- int heapsize() const
- bool isLeaf(int) const
- int leftchild(int) const
- int rightchild(int) const
- int parent(int) const
- void insert(const ELEM)
- ELEM removemax()
- ELEM remove(int)
- void buildheap()
19
Siftdown
- For fast heap construction
- Work from high end of array to low end.
- Call siftdown for each item.
- Dont need to call siftdown on leaf nodes.
- void heapbuildheap()
- for (int in/2-1 igt0 i--) siftdown(i)
- void heapsiftdown(int pos)
- assert((posgt0) (posltn))
- while (!isleaf(pos))
- int jleftchild(pos)
- if ((jlt(n-1) key(Heapj)ltkey(Heapj1)))
- j // j now has position of child with greater
value - if (key(Heappos)gtkey(Heapj)) return
- swap(Heappos, Heapj)
- posj
20
Priority Queues
- A priority queue stores objects and on request,
releases the object with the greatest value. - Example scheduling jobs in a multi-tasking
operating system. - The priority of a job may change, requiring some
reordering of the jobs. - Implementation use a heap to store the priority
queue. - To support priority reordering, delete and
re-insert. Need to know index for the object. - ELEM heapremove(int pos)
- assert((posgt0) (posltn))
- swap (Heappos, Heap--n)
- if (n!0)
- siftdown(pos)
- return Heapn