Approximation methods in Quantum Mechanics

1
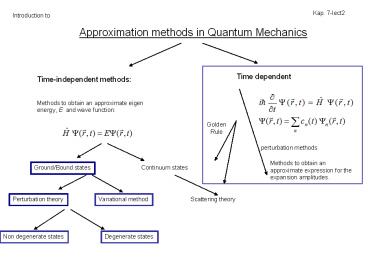
Approximation methods in Quantum Mechanics
Kap. 7-lect2
Introduction to
Time dependent
Time-independent methods
Methods to obtain an approximate eigen energy, E
and wave function
Golden Rule
perturbation methods
Methods to obtain an approximate expression for
the expansion amplitudes.
Ground/Bound states
Continuum states
Perturbation theory
Variational method
Scattering theory
Non degenerate states
Degenerate states
2
Scattering Theory

• Classical Scattering
• Differential and total cross section
• Examples Hard sphere and Coulomb scattering

• Quantal Scattering
• Formulated as a stationary problem
• Integral Equation
• Born Approximation
• Examples Hard sphere and Coulomb scattering

3
The Scattering Cross Section (To be corrected,
see Endre Slide)
per unit time
Differential Cross Section
Total Cross Section
Dimension AreaInterpretation Effective area
for scattering.
4
The Scattering Cross Section
Differential Cross Section
Total Cross Section
5
Quantal Scattering - No Trajectory! (A plane
wave hits some object and a spherical wave
emerges)
Procedure

• Solve the time independent Schrödinger equation
• Approximate the solution to one which is valid
  far away from the scattering center
• Write the solution as a sum of an incoming plane
  wave and an outgoing spherical wave.
• Must find a relation between the wavefunction and
  the current densities that defines the cross
  section.

6
Current Density
Incomming current density
Outgoing spherical current density
7
(No Transcript)
8
Example - Classical scattering
Hard Sphere scattering
Geometrical Cross sectional area of sphere!
Independent of angles!
9
(No Transcript)
10
(No Transcript)
11
Example from 1D
In this case (since potential is discontinuous)
we can find f excactly by gluing
12
The Schrödinger equation - scattering form
Now we must define the current densities from the
wave function
13
The final expression
14
Summary

Then we have
. Now we can start to work
15
Integral equation
With the rewritten Schrödinger equation we can
introducea Greens function, which (almost)
solves the problem for a delta-function
potential
Then a solution of
can be written
where we require
because.
16
This term is 0
This equals
Integration over the delta function gives result
Formal solution
Useless so far!
17
Must find G(r) in
Note
Then
The function
solves the problem!
Proof
The integral can be evaluated, and the result is
18
implies that
Inserting G(r), we obtain
At large r this can be recast to an outgoing
spherical wave..
The Born series
And so on. Not necesarily convergent!
19
SUMMARY
We obtains
At large r this can be recast to an outgoing
spherical wave..
The Born series
And so on. Not necesarily convergent!
20
Asymptotics - Detector is at near infinite r
The potential is assumed to have short range,
i.e. Active only for small r
1)
2)
Asymptotic excact result
Still Useless!
21
The Born approximation
The scattering amplitude is then
) The momentum change Fourier transform of the
potential!
Valid when
Weak potentials and/or large energies!
22
Spheric Symmetric potentials
Total Cross Section
23
Summary - 1st. Born Approximation
Best at large energies!
24
Example - Hard sphere 1. Born scattering
Classical Hard Sphere scattering
Quantal Hard Sphere potential
Thats it!
Depends on angles - but roughly independent when
qR ltlt 1