Image Transforms - PowerPoint PPT Presentation
Title:
Image Transforms
Description:
Image Transforms Basic idea Input Image, I(x,y) (spatial domain) Mathematical Transformation F( ) Transformed Image F(u, v) Processing F(u,v) Inverse Transformation – PowerPoint PPT presentation
Number of Views:266
Avg rating:3.0/5.0
Title: Image Transforms
1
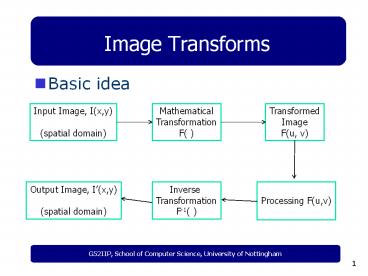
Image Transforms
- Basic idea
Input Image, I(x,y) (spatial domain)
Mathematical Transformation F( )
Transformed Image F(u, v)
Processing F(u,v)
Inverse Transformation F-1( )
Output Image, I(x,y) (spatial domain)
2
Image Transforms
- Fourier Transform
- There are many different transformations, Fourier
Transform (FT) or its fast implementation (FFT)
is the most well-known. - For the purpose of this course, we will treat FFT
as a black box, and will not go through the
detail mathematics (i.e., not required). - Instead of formal mathematics, which will be more
elegant, we will try to explain the essential
idea of FFT informally.
3
Image Transforms
- Fourier Transform Essential idea
- Any given function (an image is a 2D function)
can be approximated by a weighted sum of sines
and conses.
4
Image Transforms
- Fourier Transform
- Basic idea
4
5
Image Transforms
f(t)
Cos(2?t)
f(t)
f(t) Cos(?t/2)Cos(?t)Cos(2?t)
Cos(?t)
Cos(?t/2)
6
Image Transforms
f(t)
- In general,
- The weight, Fi, indicates the importance of
cos(uit) - ui represents the frequency of the cosine signal
- A larger ui, cos(uit) changes faster -gt higher
frequency component of f(t) - A smaller ui, cos(uit) changes slower -gt lower
frequency component of f(t)
7
Image Transforms
f(t)
Cos(2?t)
f(t) Cos(?t/2)Cos(?t)Cos(2?t) F1 1 u1
?/2 F2 1 u2 ? F3 1 u3 2?
Cos(?t)
Cos(?t/2)
8
Image Transforms
f(t)
Cos(2?t)
f(t) 5Cos(?t/2)2Cos(?t)Cos(2?t) F1
5 u1 ?/2 F2 2 u2 ? F3 1 u3 2?
Cos(?t)
Cos(?t/2)
9
Image Transforms
f(t)
Cos(2?t)
f(t) Cos(?t/2)2Cos(?t)5Cos(2?t) F1
1 u1 ?/2 F2 2 u2 ? F3 5 u3 2?
Cos(?t)
Cos(?t/2)
10
Image Transforms
f(t)
F1 1 u1 ?/2 F2 2 u2 ? F3 5 u3 2?
F1 5 u1 ?/2 F2 2 u2 ? F3 1 u3 2?
F1 1 u1 ?/2 F2 1 u2 ? F3 1 u3 2?
f(t) F1Cos(?t/2)F3Cos(?t)F3Cos(2?t)
11
Image Transforms
f(t)
F1 1 u1 ?/2 F2 2 u2 ? F3 5 u3 2?
F1 5 u1 ?/2 F2 2 u2 ? F3 1 u3 2?
F1 1 u1 ?/2 F2 1 u2 ? F3 1 u3 2?
f(t) F1Cos(?t/2)F3Cos(?t)F3Cos(2?t)
12
Image Transforms
f(t)
F1 1 u1 ?/2 F2 2 u2 ? F3 5 u3 2?
F1 5 u1 ?/2 F2 2 u2 ? F3 1 u3 2?
F1 1 u1 ?/2 F2 1 u2 ? F3 1 u3 2?
Power spectrum or Frequency Distribution
f(t) F1Cos(?t/2)F3Cos(?t)F3Cos(2?t)
13
Image Transforms
f(t)
F1 1 u1 ?/2 F2 2 u2 ? F3 5 u3 2?
F1 5 u1 ?/2 F2 2 u2 ? F3 1 u3 2?
F1 1 u1 ?/2 F2 1 u2 ? F3 1 u3 2?
What can we tell about the function (image) from
its frequency distribution?
f(t) F1Cos(?t/2)F3Cos(?t)F3Cos(2?t)
14
Image Transforms
f(t)
- Fourier Transform so far our informal
illustration
f(t)
FFT
F(u)
FFT
15
Image Transforms
f(t)
- Fourier Transform Actual
A continuous function rather than discrete
f(t)
FFT
F(u)
F(u)
FFT
u
16
Image Transforms
f(t)
- Fourier Transform Actual
F(u)
u
Similar to the discrete case, from F(u), we can
tell something about the signal f(t)
F(u)
u
17
Image Transforms
f(t)
- Fourier Transform To summaries
- From F(u), we can tell something about its
spatial signal, whether it contains fast/slow
changing features
f(t)
FFT
F(u)
F(u)
FFT
18
Image Transforms
- Now, come back to the idea of frequency domain
processing - F( )
Input Image, I(x,y) (spatial domain)
Mathematical Transformation F( )
Transformed Image F(u, v)
F
Processing F(u,v)
Inverse Transformation F( )
Output Image, I(x,y) (spatial domain)
19
Image Transforms
- Now, come back to the idea of frequency domain
processing - F( )
To achieve smoothing, low-pass filtering, we
attenuate the higher frequency part of F(u)
Input Image, I(x,y) (spatial domain)
Mathematical Transformation F( )
Transformed Image F(u, v)
F
Processing F(u,v)
Inverse Transformation F( )
Output Image, I(x,y) (spatial domain)
20
Image Transforms
- Now, come back to the idea of frequency domain
processing - F( )
To achieve sharpening, low-pass filtering, we
attenuate the lower frequency part of F(u)
Input Image, I(x,y) (spatial domain)
Mathematical Transformation F( )
Transformed Image F(u, v)
F
Processing F(u,v)
Inverse Transformation F( )
Output Image, I(x,y) (spatial domain)
21
Image Transforms
- Band limiting signals A signals Fourier
transform equal to zero above a certain finite
frequency - All images (natural signals) are band limiting
signals
F(u)
22
Frequency Domain Processing
im
- In practice
- Matlab
- f2fft2(im)
- f2fftshift(f2)
- fabs2FH_abs(f2)
- (calculate magnitude,
- FFT are complex number)
- imshow(fabs2)
23
Frequency Domain Processing
- Another
- example
24
Convolution and Spatial Filtering
- Spatial filtering is the convolution between the
input image and the filtering mask
f(x,y)
w(x,y)
f(x,y)w(x,y)
25
Frequency Domain Processing
- The foundation of frequency domain techniques is
the convolution theorem
26
Frequency Domain Processing
H(u, v) is called the transfer function
27
Frequency Domain Processing
- Typical lowpass filters and their transfer
functions
28
Frequency Domain Processing
- Typical lowpass filters and their transfer
functions
29
Frequency Domain Processing
- Example
30
Frequency Domain Processing
- Example
31
Frequency Domain Processing
- Typical lowpass filters and their transfer
functions
32
Frequency Domain Processing
- Example
33
Frequency Domain Processing
- Typical lowpass filters and their transfer
functions
34
Frequency Domain Processing
- Example
35
Frequency Domain Processing
- Example
36
Frequency Domain Processing
- Example
37
Frequency Domain Processing
- Typical highpass filters and their transfer
functions
38
Frequency Domain Processing
- Typical highpass filters and their transfer
functions
39
Frequency Domain Processing
- Typical highpass filters and their transfer
functions
40
Frequency Domain Processing
- Examples
41
Frequency Domain Processing
- Examples
42
Frequency Domain Processing
- Examples
43
Frequency Domain Processing
- More examples
44
Frequency Domain Processing
- Examples
45
Frequency Domain Processing
- Examples
46
Frequency Domain Processing
- Spatial vs frequency domain
47
Frequency Domain Processing
- Spatial vs frequency domain
48
Frequency Domain Processing
- Examples