Skewness

1
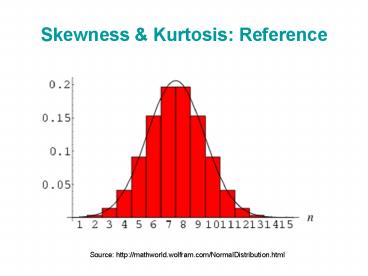
Skewness Kurtosis Reference
Source http//mathworld.wolfram.com/NormalDistrib
ution.html
2
Further Moments Skewness

• Skewness measures the degree of asymmetry
  exhibited by the data
• If skewness equals zero, the histogram is
  symmetric about the mean
• Positive skewness vs negative skewness
• Skewness measured in this way is sometimes
  referred to as Fishers skewness

3
Further Moments Skewness
Source http//library.thinkquest.org/10030/3smods
as.htm
4
Median
Mean
A
B
5
n 26 mean 4.23 median 3.5 mode 8
6
Value Occurrences Deviation Cubed
deviation OccurCubed
1 1 (1 4.23) -3.23 (-3.23)3 -33.70
-33.70 2 4 (2 4.23) -2.23 (-2.23)3
-11.09 -44.36 3 8 (3 4.23) -1.23 (-1.13)3
-1.86 -14.89 4 4 (4 4.23) -0.23 (-0.23)3
-0.01 -0.05 5 3 (5 4.23)
0.77 (0.77)3 0.46 1.37 6 2 (6 4.23)
1.77 (1.77)3 5.54 11.09 7 1 (7
4.23) 2.77 (2.77)3 21.25 21.25 8 1 (8
4.23) 3.77 (3.77)3 53.58 53.58 9 1 (9
4.23) 4.77 (4.77)3 108.53 108.53 10 1 (10 -
4.23) 5.77 (5.77)3 192.10 192.10
Sum 294.94
Mean 4.23 s 2.27
Skewness 0.97
7
Median
Mean
Skewness gt 0 (Positively skewed)
8
Mode
Median
Mean
A
B
Skewness lt 0 (Negatively skewed)
9
Source http//mathworld.wolfram.com/NormalDistrib
ution.html
Skewness 0 (symmetric distribution)
10
Skewness Review

• Positive skewness
• There are more observations below the mean than
  above it
• When the mean is greater than the median
• Negative skewness
• There are a small number of low observations and
  a large number of high ones
• When the median is greater than the mean

11
Kurtosis Review

• Kurtosis measures how peaked the histogram is
  (Karl Pearson, 1905)
• The kurtosis of a normal distribution is 0
• Kurtosis characterizes the relative peakedness or
  flatness of a distribution compared to the normal
  distribution

12
Kurtosis Review

• Platykurtic When the kurtosis lt 0, the
  frequencies throughout the curve are closer to be
  equal (i.e., the curve is more flat and wide)
• Thus, negative kurtosis indicates a relatively
  flat distribution
• Leptokurtic When the kurtosis gt 0, there are
  high frequencies in only a small part of the
  curve (i.e, the curve is more peaked)
• Thus, positive kurtosis indicates a relatively
  peaked distribution

13
(No Transcript)
14
Source http//espse.ed.psu.edu/Statistics/Chapter
s/Chapter3/Chap3.html
15
Measures of central tendency Review

• Measures of the location of the middle or the
  center of a distribution
• Mean
• Median
• Mode

16
Mean Review

• Mean Average value of a distribution Most
  commonly used measure of central tendency
• Median This is the value of a variable such
  that half of the observations are above and half
  are below this value, i.e., this value divides
  the distribution into two groups of equal size
• Mode - This is the most frequently occurring
  value in the distribution

17
An Example Data Set

• Daily low temperatures recorded in Chapel Hill
  (01/18-01/31, 2005, F)
• Jan. 18 11 Jan. 25 25
• Jan. 19 11 Jan. 26 33
• Jan. 20 25 Jan. 27 22
• Jan. 21 29 Jan. 28 18
• Jan. 22 27 Jan. 29 19
• Jan. 23 14 Jan. 30 30
• Jan. 24 11 Jan. 31 27
• For these 14 values, we will calculate all three
  measures of central tendency - the mean, median,
  and mode

18
Mean Review

• Mean Most commonly used measure of central
  tendency
• Procedures
• (1) Sum all the values in the data set
• (2) Divide the sum by the number of values in the
  data set
• Watch for outliers

19
Mean Review

• (1) Sum all the values in the data set
• ? 11 11 11 14 18 19 22 25 25
  27 27 29 30 33 302
• (2) Divide the sum by the number
• of values in the data set
• ? Mean 302/14 21.57
• Is this a good measure of central tendency for
  this data set?

20
Median Review

• Median - 1/2 of the values are above it 1/2
  below
• (1) Sort the data in ascending order
• (2) Find the value with an equal number of values
  above and below it
• (3) Odd number of observations ? (n-1)/21
  value from the lowest
• (4) Even number of observations ? average (n/2)
  and (n/2)1 values
• (5) Use the median with asymmetric distributions,
  particularly with outliers

21
Median Review

• (1) Sort the data in ascending order
• ? 11, 11, 11, 14, 18, 19, 22, 25, 25, 27, 27,
  29, 30, 33
• (2) Find the value with an equal number of values
  above and below it
• Even number of observations ? average the (n/2)
  and (n/2)1 values
• ? (14/2) 7 (14/2)1 8
• ? (2225)/2 23.5 (F)
• Is this a good measure of central tendency for
  this data?

22
Mode Review

• Mode This is the most frequently occurring
  value in the distribution
• (1) Sort the data in ascending order
• (2) Count the instances of each value
• (3) Find the value that has the most occurrences
• If more than one value occurs an equal number of
  times and these exceed all other counts, we have
  multiple modes
• Use the mode for multi-modal data

23
Mode Review

• (1) Sort the data in ascending order
• ? 11, 11, 11, 14, 18, 19, 22, 25, 25, 27, 27,
  29, 30, 33
• (2) Count the instances of each value
• ? 11, 11, 11, 14, 18, 19, 22, 25, 25, 27, 27,
  29, 30, 33
• 3x 1x 1x 1x 1x
  2x 2x 1x 1x 1x
• (3) Find the value that has the most occurrences
• ? mode 11 (F)
• Is this a good measure of the central tendency of
  this data set?

24
Measures of Dispersion Review

• In addition to measures of central tendency, we
  can also summarize data by characterizing its
  variability
• Measures of dispersion are concerned with the
  distribution of values around the mean in data
• Range
• Interquartile range
• Variance
• Standard deviation
• z-scores
• Coefficient of Variation (CV)

25
An Example Data Set

• Daily low temperatures recorded in Chapel Hill
  (01/18-01/31, 2005, F)
• Jan. 18 11 Jan. 25 25
• Jan. 19 11 Jan. 26 33
• Jan. 20 25 Jan. 27 22
• Jan. 21 29 Jan. 28 18
• Jan. 22 27 Jan. 29 19
• Jan. 23 14 Jan. 30 30
• Jan. 24 11 Jan. 31 27
• For these 14 values, we will calculate all
  measures of dispersion

26
Range Review

• Range The difference between the largest and
  the smallest values
• (1) Sort the data in ascending order
• (2) Find the largest value
• ? max
• (3) Find the smallest value
• ? min
• (4) Calculate the range
• ? range max - min
• Vulnerable to the influence of outliers

27
Range Review

• Range The difference between the largest and
  the smallest values
• (1) Sort the data in ascending order
• ? 11, 11, 11, 14, 18, 19, 22, 25, 25, 27,
  27, 29, 30, 33
• (2) Find the largest value
• ? max 33
• (3) Find the smallest value
• ? min 11
• (4) Calculate the range
• ? range 33 11 22

28
Interquartile Range Review

• Interquartile range The difference between the
  25th and 75th percentiles
• (1) Sort the data in ascending order
• (2) Find the 25th percentile (n1)/4
  observation
• (3) Find the 75th percentile 3(n1)/4
  observation
• (4) Interquartile range is the difference between
  these two percentiles

29
Interquartile Range Review

• (1) Sort the data in ascending order
• ? 11, 11, 11, 14, 18, 19, 22, 25, 25, 27, 27,
  29, 30, 33
• (2) Find the 25th percentile (n1)/4
  observation
• ? (141)/4 3.75 ? 11(14-11)0.75 13.265
• (3) Find the 75th percentile 3(n1)/4
  observation
• ? 3(141)/4 11.25 ? 27(29-27)0.25 27.5
• (4) Interquartile range is the difference between
  these two percentiles
• ? 27.5 13.265 14.235

30
Variance Review

• Variance is formulated as the sum of squares of
  statistical distances (or deviation) divided by
  the population size or the sample size minus one

31
Variance Review

• (1) Calculate the mean
• ?
• (2) Calculate the deviation for each value
• ?
• (3) Square each of the deviations
• ?
• (4) Sum the squared deviations
• ?
• (5) Divide the sum of squares by (n-1) for a
  sample
• ?

32
Variance Review

• (1) Calculate the mean
• ?
• (2) Calculate the deviation for each value
• ?
• Jan. 18 (11 25.7) -10.57 Jan. 25 (25
  25.7) 3.43
• Jan. 19 (11 25.7) -10.57 Jan. 26 (33
  25.7) 11.43
• Jan. 20 (25 25.7) 3.43 Jan. 27 (22
  25.7) 0.43
• Jan. 21 (29 25.7) 7.43 Jan. 28 (18
  25.7) -3.57
• Jan. 22 (27 25.7) 5.43 Jan. 29 (19
  25.7) -2.57
• Jan. 23 (14 25.7) -7.57 Jan. 30 (30
  25.7) 8.42
• Jan. 24 (11 25.7) -10.57 Jan. 31 (27
  25.7) 5.42

33
Variance Review

• (3) Square each of the deviations
• ?
• Jan. 18 (-10.57)2 111.76 Jan. 25
  (3.43)2 11.76
• Jan. 19 (-10.57)2 111.76 Jan. 26 (11.43)2
  130.61
• Jan. 20 (3.43)2 11.76 Jan. 27 (0.43)2
  0.18
• Jan. 21 (7.43)2 55.18 Jan. 28 (-3.57)2
  12.76
• Jan. 22 (5.43)2 29.57 Jan. 29 (-2.57)2
  6.61
• Jan. 23 (7.57)2 57.33 Jan. 30 (8.43)2
  71.04
• Jan. 24 (-10.57)2 111.76 Jan. 31 (5.43)2
  29.57
• (4) Sum the squared deviations
• ?

751.43
34
Variance Review

• (5) Divide the sum of squares by (n-1) for a
  sample
• ?

751.43 / (14-1) 57.8

• The variance of the Tmin data set (Chapel Hill)
  is 57.8

35
Standard Deviation Review

• Standard deviation is equal to the square root of
  the variance
• Compared with variance, standard deviation has a
  scale closer to that used for the mean and the
  original data

36
Standard Deviation Review

• (1) Calculate the mean
• ?
• (2) Calculate the deviation for each value
• ?
• (3) Square each of the deviations
• ?
• (4) Sum the squared deviations
• ?
• (5) Divide the sum of squares by (n-1) for a
  sample
• ?
• (6) Take the square root of the resulting
  variance
• ?

37
Standard Deviation Review

• (1) (5)
• ? s2 57.8
• (6) Take the square root of the variance
• ?
• The standard deviation (s) of the Tmin data set
  (Chapel Hill) is 7.6 (F)

38
z-score Review

• Since data come from distributions with different
  means and difference degrees of variability, it
  is common to standardize observations
• One way to do this is to transform each
  observation into a z-score
• May be interpreted as the number of standard
  deviations an observation is away from the mean

39
z-scores Review

• z-score is the number of standard deviations an
  observation is away from the mean
• (1) Calculate the mean
• ?
• (2) Calculate the deviation
• ?
• (3) Calculate the standard deviation
• ?
• (4) Divide the deviation by standard deviation
• ?

40
z-scores Review

• Z-score for maximum Tmin value (33 F)
• (1) Calculate the mean
• ?
• (2) Calculate the deviation
• ?
• (3) Calculate the standard deviation (SD)
• ?
• (4) Divide the deviation by standard deviation
• ?

41
Coefficient of Variation Review

• Coefficient of variation (CV) measures the spread
  of a set of data as a proportion of its mean.
• It is the ratio of the sample standard deviation
  to the sample mean
• It is sometimes expressed as a percentage
• There is an equivalent definition for the
  coefficient of variation of a population

42
Coefficient of Variation Review

• (1) Calculate mean
• ?
• (2) Calculate standard deviation
• ?
• (3) Divide standard deviation by mean
• ?

CV
43
Coefficient of Variation Review

• (1) Calculate mean
• ?
• (2) Calculate standard deviation
• ?
• (3) Divide standard deviation by mean
• ?

CV
44
Histograms Review

• We may also summarize our data by constructing
  histograms, which are vertical bar graphs
• A histogram is used to graphically summarize the
  distribution of a data set
• A histogram divides the range of values in a data
  set into intervals
• Over each interval is placed a bar whose height
  represents the percentage of data values in the
  interval.

45
Building a Histogram Review

• (1) Develop an ungrouped frequency table
• ? 11, 11, 11, 14, 18, 19, 22, 25, 25, 27, 27,
  29, 30, 33
• ?

11 3
14 1
18 1
19 1
22 1
25 2
27 2
29 1
30 1
33 1
46
Building a Histogram Review

• 2. Construct a grouped frequency table
• ? Select a set of classes
• ?

11-15 4
16-20 2
21-25 3
26-30 4
31-35 1
47
Building a Histogram Review

• 3. Plot the frequencies of each class

48
Box Plots Review

• We can also use a box plot to graphically
  summarize a data set
• A box plot represents a graphical summary of what
  is sometimes called a five-number summary of
  the distribution
• Minimum
• Maximum
• 25th percentile
• 75th percentile
• Median
• Interquartile Range (IQR)

49
Boxplot Review
50
Further Moments of the Distribution

• While measures of dispersion are useful for
  helping us describe the width of the
  distribution, they tell us nothing about the
  shape of the distribution

51
Skewness Review

• Skewness measures the degree of asymmetry
  exhibited by the data
• Positive skewness More observations below the
  mean than above it
• Negative skewness A small number of low
  observations and a large number of high ones

For the example data set Skewness -0.1851
52
Skewness -0.1851 (Negatively skewed)
53
Kurtosis Review

• Kurtosis measures how peaked the histogram is
• Leptokurtic a high degree of peakedness
• Values of kurtosis over 0
• Platykurtic flat histograms
• Values of kurtosis less than 0

For the example data set Kurtosis -1.54 lt 0
54
Kurtosis -1.54 lt 0 (Platykurtic)