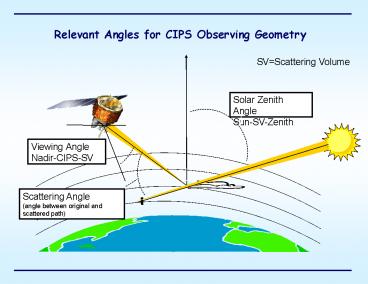
Relevant Angles for CIPS Observing Geometry

1
Relevant Angles for CIPS Observing Geometry
SVScattering Volume
Solar Zenith Angle Sun-SV-Zenith
Viewing Angle Nadir-CIPS-SV
Scattering Angle (angle between original and
scattered path)
2
Some Useful Descriptions of the Atmosphere I
Decrease in pressure with height
Pressure is the force per unit area exerted by
the atmosphere Therefore pressure could be
expressed as the weight of a column of air
molecules
ppressure, nnumber density, mmean mass of
individual molecules (.8mN2 .2mO2 in trop.)
N(z) is the column density, the number of
molecules in a column of unit area extending from
altitude z to the top of the atmosphere
Ideal gas law kBBoltzmanns constant,
Ttemperature
H is called the scale height
3
Some Useful Descriptions of the Atmosphere II
Relate pressure to height
Solve assuming constant temperature
H is the distance over which the atmospheric
pressure decreases by a factor e.
H is also then the distance over which the
atmospheric number density of molecules decreases
by a factor e.
4
Some Useful Descriptions of the Atmosphere III
How is column density related to scale height?
(assuming constant temperature)
H is also the height the atmosphere would be if
it were collapsed to a layer of uniform density
These relationships are useful for getting a feel
for how the atmosphere behaves. Because they
assume that temperature is constant, their
quantitative utility is limited. They should only
be applied in small altitude intervals. In
practice its usually better to calculate column
density by its defining equation. This is for a
vertical column.
Sometimes, what is needed is the slant column
density for a path at angle q relative to
vertical (this version works for q lt 70 degrees)
5
Optical Depth
F is irradiance s is cross section
F(l,z)
Z
t is called optical depth and describes how far a
photon is likely to travel through a column of
gas. As a flux travels a distance such that t
equals unity, the flux is reduced by a factor of
e.
6
Cross Sections
Ozone Absorption
Rayleigh Scattering
Cross Sections - have units of area represent
the size of the target for photons colliding
with atoms, molecules, or ions Dependent upon
photon energy There is one total cross section
describing the area presented by the target atom
or molecule in a collision, this cross section is
the sum of many individual cross sections that
represent probabilities or efficiencies of all
the individual possible processes (scattering,
absorption, etc.) Cross sections therefore
represent the efficiency of a given process
7
CIPS Observing Geometry for a Single Observation
A beam of solar photons travels along a path to
the scattering volume and then to CIPS. Along the
way photons are removed from the beam due to
absorption by ozone. Note that there are
contributions to the Rayleigh scattered signal
from all points along the path (these are not
shown).
8
CIPS Algorithm Overview
The observed albedo from Rayleigh scattering may
be written according to the single scattering
formula
S 1/cos(q) 1/cos(q0) q viewing angle q0
solar zenith angle X ozone density as a
function of pressure level l wavelength (265 nm
for CIPS)
Il atmospheric radiance Fl solar irradiance b
Rayleigh scattering coefficient PR Rayleigh
phase function Q scattering angle p pressure
in mb a absorption coefficient of ozone
9
We have generalized the result of McPeters et al.
1980 and shown that by assuming ozone density
varies exponentially with altitude and that the
ratio of the ozone scale height to that of the
background atmosphere is constant, then
where, Nair the air vertical column density
above 1 mb CO3 ozone column density above 1
mb m cos(q) m0 cos(q0) And s the ratio of
the ozone scale height to that of the background
atmosphere HALOE observations have shown that s
does not deviate significantly from 0.7.
10
Ozone concentration
Relative contribution to nadir viewing Rayleigh
scattered radiance
11
Cloud Albedo
where, APMC is the nadir viewing albedo of the
cloud if observed at Q 90 PM Mie Phase
Function Note that although currently not
implemented, this equation may need to be scaled
by m cos(q), this should be a topic for
consideration
12
Phase function is the fraction of radiance
emitted per unit solid angle
Mie Phase function of mean particle size
0,10,20,30,40,50, 60 nm
Rayleigh Phase Function
Phase function for Gaussian particle distribution
with width 14 nm
13
Interpreting CIPS Scattering Profile
The unknowns are CO3, s, APMC, and R Option 1
Non linear least squares fit and use 7 data
points to retrieve 4 unknowns - experience says
this is prone to significant error bars Option
2 Assume an s, use NLSfit to retrieve CO3, APMC,
and R Option 3 Have an indicator of cloud
presence if cloud not thought to be present,
solve only for CO3, s if a cloud is thought
present, assume s, solve for CO3, APMC, and
R (assumed s could be taken from observations
in cloud free regions)
14
How can we determine the presence of a cloud?
For the case of no cloud, y should be a simple
linear function of x (with a slope of s) If a
cloud is present, the slope is changed, the
effect is different for small scattering angles
versus large ones. For example, calculate slope
at small scattering angles and compare to same
calculation for large scattering angles, if ratio
is significantly different from 1, then a cloud
is likely to be present.
15
PMC (forward scattering)
Rayleigh Background
PMC (backward scattering)