Normal Distribution Starters

1
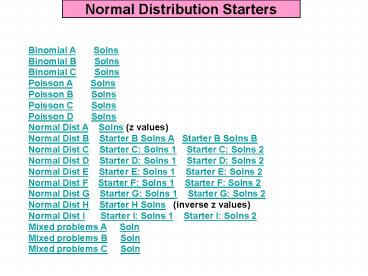
Normal Distribution Starters
Binomial A SolnsBinomial B
SolnsBinomial C SolnsPoisson A
SolnsPoisson B SolnsPoisson C
SolnsPoisson D SolnsNormal Dist A
Solns (z values)Normal Dist B Starter B Solns
A Starter B Solns BNormal Dist C Starter C
Solns 1 Starter C Solns 2Normal Dist D
Starter D Solns 1 Starter D Solns 2Normal
Dist E Starter E Solns 1 Starter E Solns
2Normal Dist F Starter F Solns 1 Starter
F Solns 2Normal Dist G Starter G Solns 1
Starter G Solns 2Normal Dist H Starter H
Solns (inverse z values) Normal Dist I
Starter I Solns 1 Starter I Solns 2Mixed
problems A SolnMixed problems B
SolnMixed problems C Soln
2
Binomial A
1st Page
1) On average one bowl in every 4 has lumpy
porridge. If big daddy B has 6 bowls of
porridge, find the probability   (a)
There are exactly 5 bowls with lumpy porridge.  
(b) There are at most 1 bowl with lumpy
porridge.       2) Goldilocks has nightmares on 4
nights each week on average.   a) Find the
probability of her having more than 2
nights with nightmares in a week.     b) Given
that she had less than 5 nightmare nights in a
week, find the probability that she had
only 1 nightmare night.
3
Binomial A Soln
1st Page
1) On average one bowl in every 4 has lumpy
porridge. If big daddy B has 6 bowls of
porridge, find the probability   (a) There
are exactly 5 bowls with lumpy porridge.   (b)
There are at most 1 bowl with lumpy
porridge.       2) Goldilocks has nightmares on 4
nights each week on average.   a) Find the
probability of her having more than 2
nights with nightmares in a week.     b) Given
that she had less than 5 nightmare nights in a
week, find the probability that she had
only 1 nightmare night.
4
Binomial B
1st Page
1) It is known that 60 of candidates will
achieve in an examination. If 5 people sit
the examination find the probability   (a)
Exactly 3 candidates will achieve.    (b) At
least 3 candidates will achieve.      2) A drug
is known to be 90 effective when it is used to
cure a disease. If 20 people are given the
drug then X is binomial with n 20, ?
0.9.   a) Find the mean on the binomial
distribution     b) Find the standard deviation
on the binomial distribution    
5
Binomial B Soln
1st Page
1) It is known that 60 of candidates will
achieve in an examination. If 5 people sit
the examination find the probability   (a)
Exactly 3 candidates will achieve.    (b) At
least 3 candidates will achieve.      2) A drug
is known to be 90 effective when it is used to
cure a disease. If 20 people are given the
drug then X is binomial with n 20, ?
0.9.   a) Find the mean on the binomial
distribution     b) Find the standard deviation
on the binomial distribution    
6
Binomial C
1st Page
1) List the conditions of the binomial
distribution.   2) It is known that 18.5 of
people can turn their eyelids inside out. In a
group of 20 people what is the probability that
more than 1 person can turn their eyelids inside
out?  
7
Binomial C Soln
1st Page
1)  Binomial distribution occurs when (a) There
is a fixed number (n) of trials. (b) The result
of any trial can be classified as a success or
a failure (c) The probability of a success (?
or p) is constant from trial to trial. (d) Trials
are independent.   P(X x) nCx ?x(1 -
?)n-x    2) It is known that 18.5 of people
can turn their eyelids inside out. In a group of
20 people what is the probability that more than
1 person can turn their eyelids inside out?  
8
Poisson A
1st Page
1) List the conditions of the Poisson
distribution.   2) In a particular marine
reserve there are on average 1.25 crayfish per m2
of seafloor. In a 20m2 area what is the
probability that there are 10 crayfish?  
9
Poisson A Soln
1st Page
1) Poisson distribution occurs when (a) Trials
are independent. (b) The events cannot occur
simultaneously (c) Events are random and
unpredictable (d) The probability of an event
occurring is proportional to the interval length
(for small intervals) 2) In a particular marine
reserve there are on average 1.25 crayfish per m2
of seafloor. In a 20m2 area what is the
probability that there are 10 crayfish?  
10
Poisson B
1st Page
1) Goldilocks breaks three chairs per hour at
school because she is over weight. What is the
probability that she breaks no more than four
chairs in an hour. (Assume chair breakages are
independent )   2) Goldilocks has on average
five tantrums per hour. What is the probability
that she has at least two tantrums in a given
fifteen minute interval. (Assume tantrums are
independent )  
11
Poisson B Soln
1st Page
1) Goldilocks breaks three chairs per hour at
school because she is over weight. What is the
probability that she breaks no more than four
chairs and an hour. (Assume chair breakages are
independent )   2) Goldilocks has on average
five tantrums per hour. What is the probability
that she has at least two tantrums in a given
fifteen minute interval. (Assume tantrums are
independent )  
12
Poisson C
1st Page

• 1) Baby bear cries four times a week on average.
  What is the mean and variance of the number of
  times he cries and a given day.
•  
• The probability that baby bears chair is not
  broken in a given week is 0.44
• What is the average number of times the chair is
  broken in a week.
• What is the standard deviation of the number of
  times the chair is broken in a week.
• What is the probability that baby bears chair is
  broken twice in a week.
•  

13
Poisson C Solns
1st Page

• 1) Baby bear cries four times a week on average.
  What is the mean and variance of the number of
  times he cries and a given day.
•  
• The probability that baby bears chair is not
  broken in a given week is 0.44
• What is the average number of times the chair is
  broken in a week.
• What is the standard deviation of the number of
  times the chair is broken in a week.
• What is the probability that baby bears chair is
  broken twice in a week.
•  

14
Poisson D
1st Page

• The bear hunting season is five months long. On
  average the bear family get angry four times a
  month in the bear hunting season and three times
  a month in the off-season.
• What is the probability that the bear family get
  angry twice in the next month?
• If the bear family did not get angry last month,
  what is the probability that it is the bear
  hunting season?
•  
•  

15
Poisson D Soln
1st Page

• The bear hunting season is five months long. On
  average the bear family get angry four times a
  month in the bear hunting season and three times
  a month in the off-season.
• What is the probability that the bear family get
  angry twice in the next month?
• If the bear family did not get angry last month,
  what is the probability that it is the bear
  hunting season?
•  
•  

16
Z values
1st Page
Look up these z values to find the
corresponding probabilities 1) P(0 lt z lt 1.4)
2) P(0 lt z lt 2.04) 3) P(0 lt z lt 1.55)
4) P(0 lt z lt 2.125)
5) P(-0.844 lt z lt 0) 6) P(-2.44 lt z lt 2.44)

7) P(-0.85 lt z lt 1.646) 8) P( z lt 2.048)
9) P(1.955 lt z lt 2.044) 10) P( z lt -2.111)
17
Z value Solutions
1st Page
Look up these z values to find the
corresponding probabilities 1) P(0 lt z lt 1.4)
2) P(0 lt z lt 2.04) 3) P(0 lt z lt 1.55)
4) P(0 lt z lt 2.125)
5) P(-0.844 lt z lt 0) 6) P(-2.44 lt z lt 2.44)

7) P(-0.85 lt z lt 1.646) 8) P( z lt 2.048)
9) P(1.955 lt z lt 2.044) 10) P( z lt -2.111)
18
Starter B
1st Page
A salmon farm water tank contains fish with a
Mean length of 240mm Calculate the probability
of the following (Std dev 15mm)
1) P(A fish is between 240 and 250mm long)
2) P(A fish is between 210 and 260mm long)
3) P(A fish is less than 254mm long)
4) P(A fish is less than 220mm long)
5) P(A fish is between 255 and 265mm long)
19
Starter B Solns 1
1st Page
A salmon farm water tank contains fish with a
Mean length of 240mm Calculate the probability
of the following (Std dev 15mm)
1) P(A fish is between 240 and 250mm long)
2) P(A fish is between 210 and 260mm long)
3) P(A fish is less than 254mm long)
20
Starter B Solns 2
1st Page
A salmon farm water tank contains fish with a
Mean length of 240mm Calculate the probability
of the following (Std dev 15mm)
4) P(A fish is less than 220mm long)
5) P(A fish is between 255 and 265mm long)
21
Starter C
1st Page
A west coast population of mosquitoes have a Mean
weight of 4.8kg Calculate the probability of the
following (Std dev 0.6kg)
1) What is the probability a mosquito is between
4.8kg and 5.8kg?
2) What percentage of mosquitoes are between 4kg
and 5kg?
3) Out of a sample of 120 mosquitoes, how many
would be over 6kg?
4) What percentage of mosquitoes are between 3kg
and 4kg?
5) What percentage of mosquitoes are under
5.5kg?
22
Starter C Solns 1
1st Page
A west coast population of mosquitoes have a Mean
weight of 4.8kg Calculate the probability of the
following (Std dev 0.6kg)
1) What is the probability a mosquito is between
4.8kg and 5.8kg?
2) What percentage of mosquitoes are between 4kg
and 5kg?
23
Starter C Solns 2
1st Page
A west coast population of mosquitoes have a Mean
weight of 4.8kg Calculate the probability of the
following (Std dev 0.6kg)
3) Out of a sample of 120 mosquitoes, how many
would be over 6kg?
4) What percentage of mosquitoes are between 3kg
and 4kg?
5) What percentage of mosquitoes are under 5.5kg?
24
Starter D
1st Page
A room contains flies with a Mean weight of 3.6g
and a Standard Deviation of 0.64kg
1) What is the probability a fly is between 3.6g
and 5.8g?
2) What percentage of flies are between 3g and 5g?
3) Out of a sample of 40 flies, how many would be
under 4g?
4) What percentage of flies are between 2g and 3g?
5) What percentage of flies are under 2.5g
25
Starter D Solns 1
1st Page
A room contains flies with a Mean weight of 3.6g
and a Standard Deviation of 0.64kg
1) What is the probability a fly is between 3.6g
and 5.8g?
2) What percentage of flies are between 3g and 5g?
26
Starter D Solns 2
1st Page
A room contains flies with a Mean weight of 3.6g
and a Standard Deviation of 0.64kg
3) Out of a sample of 40 flies, how many would be
under 4g?
4) What percentage of flies are between 2g and 3g?
5) What percentage of flies are under 2.5g
27
Starter E
1st Page
The mean weight of a loader scoop of coal is 1.25
tonnes and a standard deviation of 280 kg
1) What percentage of scoops are between 1.3 and
1.5 tonnes?
2) What percentage of scoops are less than 1
tonne?
3) Out of a sample of 500 scoops, how many would
be over 1.4 tonnes?
4) What percentage of scoops are more than 1.6
tonnes?
5) What percentage of scoops are between 1 tonne
and 2 tonnes
28
Starter E Solns 1
1st Page
The mean weight of a loader scoop of coal is 1.25
tonnes and a standard deviation of 280 kg
1) What percentage of scoops are between 1.3 and
1.5 tonnes?
2) What percentage of scoops are less than 1
tonne?
29
Starter E Solns 2
1st Page
The mean weight of a loader scoop of coal is 1.25
tonnes and a standard deviation of 280 kg
3) Out of a sample of 500 scoops, how many would
be over 1.4 tonnes?
4) What percentage of scoops are more than 1.6
tonnes?
5) What percentage of scoops are between 1 tonne
and 2 tonnes
30
Starter F
1st Page
The weight of glue paste Ralph eats in a day is
normally distributed with a mean of 4.6kg
standard deviation of 1.3kg
1) How many days in November will Ralph eat less
than 5.5kg of glue paste?
2) What percentage of days does he eat less than
4kg of glue paste?
3) Ralph vomits when he eats more than 6kg of
glue in a day. What is the chance of this
happening?
4) What percentage of days does he eat between
4.2kg and 5kg of glue?
5) What is the probability he does not eat
between 3.5 5 kg of glue paste?
31
Starter F Solns 1
1st Page
The weight of glue paste Ralph eats in a day is
normally distributed with a mean of 4.6kg
standard deviation of 1.3kg
1) How many days in November will Ralph eat less
than 5.5kg of glue paste?
2) What percentage of days does he eat less than
4kg of glue paste?
32
Starter F Solns 2
1st Page
The weight of glue paste Ralph eats in a day is
normally distributed with a mean of 4.6kg
standard deviation of 1.3kg
3) Ralph vomits when he eats more than 6kg of
glue in a day. What is the chance of this
happening?
4) What percentage of days does he eat between
4.2kg and 5kg of glue?
5) What is the probability he does not eat
between 3.5 5 kg of glue paste?
33
Starter G
1st Page
Itchy Scratchy have a hammer collection which
is normally distributed with a mean of 10.4 kg
standard deviation of 2.3kg
1) What percentage of the hammers weigh less than
8kg?
2) What is the probability a hammer weighs
between 11kg 14kg?
3) Scratchys head splits open if the hammer is
more than 15kg. What is the chance of this
happening?
4) A truck is loaded with 200 hammers. How many
of these would be 12kg or less?
5) 90 of hammers weigh more than what weight?
34
Starter G Solns 1
1st Page
Itchy Scratchy have a hammer collection which
is normally distributed with a mean of 10.4 kg
standard deviation of 2.3kg)
1) What percentage of the hammers weigh less than
8kg?
2) What is the probability a hammer weighs
between 11kg 14kg?
35
Starter G Solns 2
1st Page
Itchy Scratchy have a hammer collection which
is normally distributed with a mean of 10.4 kg
standard deviation of 2.3kg)
3) Scratchys head splits open if the hammer is
more than 15kg. What is the chance of this
happening?
4) A truck is loaded with 200 hammers. How many
of these would be 12kg or less?
5) 90 of hammers weigh more than what weight?
36
Inverse Z values
1st Page
Look up these probabilities to find the
corresponding z values 1) 2)
0.4
0.3
3) 4)
0.85
0.45
5) 6)
0.65
0.08
7) 8)
0.12
0.02
37
Inverse Z values Solns
1st Page
Look up these probabilities to find the
corresponding z values 1) 2)
0.4
0.3
3) 4)
0.85
0.45
5) 6)
0.65
0.08
7) 8)
0.12
0.02
38
Starter I
1st Page
Kenny is practicing to be in a William Tell play.
He suffers some blood loss which is normally
distributed with a mean of 120mL standard
deviation of 14mL
1) What is the probability his blood loss is less
than 100mL?
2) 80 of the time his blood loss is more then
M mL. Find the value of M
3) Kenny passes out when his blood loss is too
much. This happens 5 of the time. What is
the maximum amount of blood loss Kenny can
sustain?
4) 30 of the time Kenny is not concerned by his
blood loss? What is his blood loss when he
starts to be concerned?
5) The middle 80 of blood losses are between
what two amounts?
39
Starter I Solns 1
1st Page
Kenny is practicing to be in a William Tell play.
He suffers some blood loss which is normally
distributed with a mean of 120mL standard
deviation of 14mL
1) What is the probability his blood loss is less
than 100mL?
2) 80 of the time his blood loss is more then
M mL. Find the value of M
3) Kenny passes out when his blood loss is too
much. This happens 5 of the time. What is
the maximum amount of blood loss Kenny can
sustain?
40
Starter I Solns 2
1st Page
Kenny is practicing to be in a William Tell play.
He suffers some blood loss which is normally
distributed with a mean of 120mL standard
deviation of 14mL
4) 30 of the time Kenny is not concerned by his
blood loss? What is his blood loss when he
starts to be concerned?
5) The middle 80 of blood losses are between
what two amounts?
Lucky Kenny is not involved in the knife catching
competition!
41
Mixed Problems A
1st Page
1) Mean maximum temperature is 26C Standard
deviation 5C Temp measured to nearest
degree. a) P(Temperature at least
30C)        b) P(Temperature between 20 and
30C)        c) P(Temperature between 20 and
24C inclusive)      2) On average there are 4
frogs per litre of swamp water. What is the
probability there are less than 4 frogs in a 2
litre bucket of swamp water  
42
Mixed Problems A Soln
1st Page
1) Mean maximum temperature is 26C Standard
deviation 5C Temp measured to nearest
degree. a) P(Temperature at least
30C)        b) P(Temperature between 20 and
30C)        c) P(Temperature between 20 and
24C inclusive)      2) On average there are 4
frogs per litre of swamp water. What is the
probability there are less than 4 frogs in a 2
litre bucket of swamp water  
43
Mixed Problems B
1st Page
The mean weight of a cake is 1.5kg with standard
deviation of 0.34kg Homer weighs 120kg. 1) If
Homer ate six cakes what is the mean and standard
deviation of his total weight . 2) What is
the probability Homer weighs over 130kg?
 
44
Mixed Problems B Soln
1st Page
The mean weight of a cake is 1.5kg with standard
deviation of 0.34kg Homer weighs 120kg. 1) If
Homer ate six cakes what is the mean and standard
deviation of his total weight . 2) What is
the probability Homer weighs over 130kg?
 
45
Mixed Problems C
1st Page

• Each day Homer is exposed to radiation for six
  minutes on average (variance of 1.5 minutes)
• Radiation exposure is considered dangerous if it
  is for more than five minutes per day.
• What is the probability that Homer is exposed to
  dangerous levels of radiation on two consecutive
  days
• What is the probability that Homer is exposed to
  dangerous levels of radiation for at least three
  days in a five day week
•  

46
Mixed Problems C Soln
1st Page

• Each day Homer is exposed to radiation for six
  minutes on average (variance of 1.5 minutes)
• Radiation exposure is considered dangerous if it
  is for more than five minutes per day.
• What is the probability that Homer is exposed to
  dangerous levels of radiation on two consecutive
  days
• What is the probability that Homer is exposed to
  dangerous levels of radiation for at least three
  days in a five day week
•