11. Stability of Closed-Loop Control Systems

1
11. Stability of Closed-Loop Control Systems

• In this chapter, we analyze the stability
  characteristics of closed-loop system and present
  several useful criteria for determining whether a
  system will be stable.

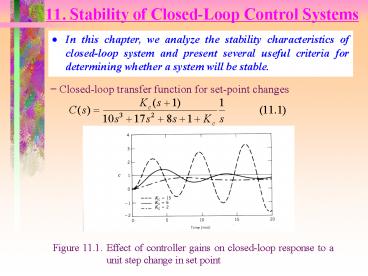
- Closed-loop transfer function for set-point
changes
Figure 11.1. Effect of controller gains on
closed-loop response to a unit step change in set
point
2
11.1 General Stability Criterion

• Open loop stable (Self-regulating) process
• the stable process without feedback
  control
• Definition of stability(BIBO Stability)

An unconstrained linear system is said to be
stable if the output response is bounded for all
bounded inputs. Otherwise it is said to be
unstable.
Example
Figure 11.2. A liquid storage system which is not
self-regulating
3
Transfer function relating liquid level h to
inlet flow rate qi
For a step change of magnitude M0 ,
Taking the inverse Laplace transform gives the
transient response,
Since this response is unbounded, we conclude
that the liquid storage system is open-loop
unstable (or non-self-regulating) since a bounded
input has produced an unbounded response.
However, if the pump in Fig.11.2 were replaced
by a valve, then the storage system would be
self-regulating.
4
11.1.1 Characteristic Equation
In Chapter 10
where, GOL GcGvGpGm
For set-point changes, Eq. (11-5) reduces as
where, m ? n for physical realizability
From Eq. (11-6) the poles are also the roots of
the following equation which is called as the
characteristic equation
1 GOL 0 ? plays a decisive role in
determining system stability
5
If R(s) 1/s and there are no repeated poles,
then
Thus, one of the poles is a positive real number,
c(t) is unbounded. If pk is akjbk, imaginary
part causes the oscillatory response and with a
positive real part, then the system is unstable.

• General Stability Criterion

The conventional feedback control system is
stable if and only if all roots of the
characteristic equation are negative or have
negative real parts. Otherwise, the system is
unstable.
6
Figure 11.3. Stability regions in the complex
plane for roots of the characteristic equation

• Note) The same characteristic equation occurs for
  both load and set-point changes since the term, 1
  GOL. Thus, if the closed-loop system is stable
  for load disturbance, it will also be stable for
  set-point changes.

7
Figure 11.4. Contributions of characteristic
equation roots to closed-loop response.
8
11.2 Routh Stability Criterion
Concept an analytical technique for
determining whether any roots of polynomial have
positive real parts
Method
Characteristic Equation ansn an-1sn-1
a1s a0 0 (angt0) 1) all the coefficients an ,
an-1 , a0 must be positive. (if any
coefficient is negative or zero, then the system
is unstable.) 2) construct Routh array
9
where, n is the order of characteristic equation,
All of the elements in the left column of the
Routh array are positive
? only valid if characteristic equation is in
polynomial of s (no time delay). ? if system
contain time delays use Pade approximation. Note)
A exact stability analysis of system containing
time delays will be treated in the frequency
analysis.
10
11.3 Direct Substitution Method
Concept Substituting s jw into the
characteristic equation ? find a stability unit
such as the maximum value of Kc .

• Example
• Use the direct-substitution method to determine
  Kcm for the system with the characteristic
  equation given by.
• 10s3 17s2 8s 1 Kc 0
  (11.9)

Solution Substitute s jw and Kc Kcm into
Eq.(11-9) -10jw3 - 17w2 8jw 1 Kcm 0
or (1 Kcm - 17w2) j(8w
-10w3) 0 (11.10) Equation
(11.10) is satisfied if both real and imaginary
parts of (11.10) are identically zero 1 Kcm -
17w2 0, 8w -10w3 0 Therefore, w ?0.894 ?
Kcm 12.6
11

• Thus, we conclude that Kc lt 12.6 for stability.
• w ?0.894 indicates that at the stability limit
  (where Kc Kcm 12.6), a sustained oscillation
  occurs that has a frequency of w 0.894
  radians/min if the time constants have units of
  minutes.
• (Recall that a pair of complex roots on the
  imaginary axis, , results in an undamped
  oscillation of frequency w.)
• The corresponding period P is P 2p/0.894 7.03
  min.

12
11.4 Root Locus Diagrams
In the design and analysis of control systems, it
is instructive to know how the roots of the
characteristic equation change when a particular
system parameter such as controller gain changes.

• A root locus diagram provides a convenient
  graphical display of this information.

Example) Consider a feedback control system that
has the following open-loop transfer function.
Plot the root locus diagram for 0 ? Kc ? 40
13
Solution The C. E. is (s 1)(s 2)(s 3)
2Kc 0.
Figure 11.5. Root locus diagram for third-order
system.

• From the above root locus diagram,
• The closed-loop system is underdamped one for Kc
  gt 0.2.
• The closed-loop system is unstable for Kc gt 30.

• Disadvantage of root locus analysis.
• ? cannot handle time delay. Thus, use the Pade
  approximation.
• ? require iterative solution of the nonlinear and
  nonrational characteristic equation (but not
  easy).

14

• Approximation by an underdamped second-order
  system.
• If the two closest roots are a complex conjugate
  pair, then the closed-loop system can be
  approximated by an under-damped second-order
  system.

From C. E.
These roots are shown in Fig. 11. 6
Figure 11.6. Root location for underdamped
second-order system