Image Restoration - PowerPoint PPT Presentation
1 / 50
Title:
Image Restoration
Description:
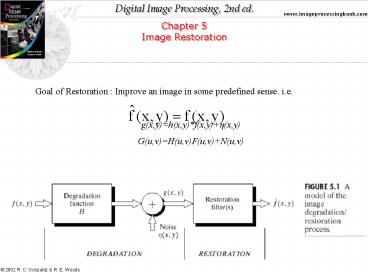
Chapter 5 Image Restoration Goal of Restoration : Improve an image in some predefined sense. i.e. g(x,y)=h(x,y)*f(x,y)+ (x,y) G(u,v)=H(u,v)F(u,v)+N(u,v) – PowerPoint PPT presentation
Number of Views:250
Avg rating:3.0/5.0
Title: Image Restoration
1
Chapter 5 Image Restoration
Goal of Restoration Improve an image in some
predefined sense. i.e. g(x,y)h(x,y)f(x,y)?(x,
y) G(u,v)H(u,v)F(u,v)N(u,v)
2
Chapter 5 Image Restoration
3
Chapter 5 Image Restoration
This test pattern is well-suited for illustrating
the noise models, because it is composed of
simple, constant areas that span the grey scale
from black to white in only three increments.
This facilitates visual analysis of the
characteristics of the various noise components
added to the image.
4
Chapter 5 Image Restoration
5
Chapter 5 Image Restoration
6
Chapter 5 Image Restoration
7
Chapter 5 Image Restoration
8
Chapter 5 Image Restoration
9
Chapter 5 Image Restoration
10
Chapter 5 Image Restoration
11
Chapter 5 Image Restoration
12
Chapter 5 Image Restoration
13
Chapter 5 Image Restoration
14
Chapter 5 Image Restoration
15
Chapter 5 Image Restoration
16
Chapter 5 Image Restoration
Periodic Noise Reduction by Frequency Domain
Filtering
- LPF HPF ? Image Enhancement
- Bandreject Filters
- 1-1) Ideal
D(u,v) distance from the origin of the centered
frequency rectangle W bandwidth D0 radial
center
17
Chapter 5 Image Restoration
Periodic Noise Reduction by Frequency Domain
Filtering
1-2) Butterworth of order n
1-3) Gaussian
18
Chapter 5 Image Restoration
19
Chapter 5 Image Restoration
20
Chapter 5 Image Restoration
Periodic Noise Reduction by Frequency Domain
Filtering
- Bandreject Filters
- Hbp(u,v)1-Hbr(u,v)
- It helps isolate the noise pattern.
21
Chapter 5 Image Restoration
22
Chapter 5 Image Restoration
Periodic Noise Reduction by Frequency Domain
Filtering
3) Notch Filters 3-1) Ideal
The center of the frequency rectangle has been
shifted to the point (M/2,N/2)
23
Chapter 5 Image Restoration
Periodic Noise Reduction by Frequency Domain
Filtering Notch Filters
3-2) Butterworth of order n
3-3) Gaussian
24
Chapter 5 Image Restoration
25
Chapter 5 Image Restoration
26
Chapter 5 Image Restoration
Periodic Noise Reduction by Frequency Domain
Filtering
4) Optimum Notch Filters
To obtain w(x,y) the goal is to minimize the
variance in the neighborhood of x,y in the image.
27
Chapter 5 Image Restoration
28
Chapter 5 Image Restoration
29
Chapter 5 Image Restoration
30
Chapter 5 Image Restoration
31
Chapter 5 Image Restoration
Linear, Position-Invariant Degradations
Estimation the Degradation Function 1) Estimation
by Image Observation
Assuming that the effect of noise is negligible.
32
Chapter 5 Image Restoration
Linear, Position-Invariant Degradations
Estimation the Degradation Function 2) Estimation
by Experimentation
A impulse Fourier transform which is constant.
33
Chapter 5 Image Restoration
34
Chapter 5 Image Restoration
Linear, Position-Invariant Degradations
Estimation the Degradation Function 3) Estimation
by modeling Turbulence model Mathematical
model
35
Chapter 5 Image Restoration
36
Chapter 5 Image Restoration
37
Chapter 5 Image Restoration
- How to get F(u,v) from degraded image G(u,v)
- Inverse Filtering
We should know N(u,v) to use this method. We
should use this method near origin because H(u,v)
is near zero in other areas.
38
Chapter 5 Image Restoration
39
Chapter 5 Image Restoration
How to get F(u,v) from degraded image G(u,v)
2) Wiener (Minimum mean square Error) Filtering
H(u,v) degradation function Sn(u,v)N(u,v)2 po
wer spectrum of the noise Sf(u,v)F(u,v)2 power
spectrum of the undergraded image
40
Chapter 5 Image Restoration
If Sf(u,v) is not known
41
Chapter 5 Image Restoration
42
Chapter 5 Image Restoration
43
Chapter 5 Image Restoration
How to get F(u,v) from degraded image G(u,v)
3) Constrained Least Squares Filtering
44
Chapter 5 Image Restoration
45
Chapter 5 Image Restoration
46
Chapter 5 Image Restoration
- Geometric Transformations (rubber-sheet
transformations) - 1) Spatial Transformations
- 2) Gray-level Transformations
47
Chapter 5 Image Restoration
48
Chapter 5 Image Restoration
49
Chapter 5 Image Restoration
50
Chapter 5 Image Restoration