Tree

1
Tree

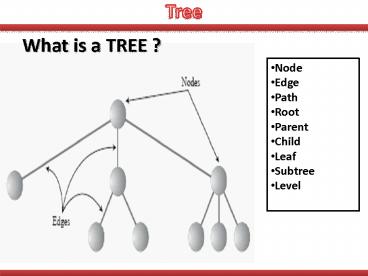
• What is a TREE ?

• Node
• Edge
• Path
• Root
• Parent
• Child
• Leaf
• Subtree
• Level

2
(No Transcript)
3
Tree

• Tree
• Tree generally implemented in the computer using
  pointers
• Unbalanced Trees means that
• Most of the nodes are on one side of the root.
• Individual subtrees may also be unbalanced.

4
Binary Tree

• Binary Tree
• It is a tree whose nodes have two children
  (possibly empty), and each child is designed as
  either a left child or a right child.

5
Operations on a Binary Tree

1. Finding node(Binary Search Tree)
2. Inserting node
3. Deleting Node
4. Traversing
5. Finding Minimum and Maximum Values

6
Operations on a Binary Tree

• 1.Finding node

57
7
Operations on a Binary Tree

• 2.Inserting node

45
8
Operations on a Binary Tree

• 3.Deleting Node
• A- The node to be deleted has no children

9
Operations on a Binary Tree

• 3.Deleting Node
• B- The node to be deleted has one child

10
Operations on a Binary Tree
         

• 3.Deleting Node
• C- The node to be deleted has two children

11
4.Traversing the Tree
Operations on a Binary Tree

• Visiting each node in a specified order.
• Three simple ways to traverse a tree
• Inorder
• Preorder
• Postorder

12
Inorder traversal the left child is recursively
visited, the node is visited, and the right child
is recursively visited.Steps involved in
Inorder traversal (recursion) are1. Call itself
to traverse the nodes left subtree2. Visit the
node (e.g. display a key)3 Call itself to
traverse the nodes right subtree.
Operations on a Binary Tree

• Void inOrder(Node pRoot)
• If (pRoot! null)
• inOrder(pRoot-gtleftChild)
• coutltlt pRoot-gtDataltlt
• inOrder(pRoot-gtrightChild)

13
Preorder traversal a node is visited and then
its children are visited recursively. Sequence
of preorder traversal -- Visit the node-- Call
itself to traverse the nodes left subtree--
Call itself to traverse the nodes right
subtree.
Operations on a Binary Tree

• Void preorder (Node pRoot)
• If (pRoot! null)
• coutltlt pRoot-gtDataltlt
• preorder (pRoot-gtleftChild)
• preorder (pRoot-gtrightChild)

14
Postorder traversal a node is visited after
both children are visited.Sequence of postorder
traversal-- Call itself to traverse the nodes
left subtree-- Call itself to traverse the
nodes right subtree-- Visit the node.
Operations on a Binary Tree

• Void Postorder (Node pRoot)
• If (pRoot! null)
• Postorder (pRoot-gtleftChild)
• Postorder (pRoot-gtrightChild)
• coutltlt pRoot-gtDataltlt

15
Binary Search Tree

• 5.Finding Minimum Values

16
Binary Search Tree

• 6.Finding Maximum Values

17
Representing the Tree in C Code
The Node Class
class Node public int day float temp Node
pLeftchild Node pRightchild //constructor Nod
e(int d,float t) day d temp t pLeftchild
NULL pRightchild NULL //display the data
as1, 5.76 void displaynode() coutltlt''ltltdayltlt'
,'ltlttempltlt'' //end class node
18
Representing the Tree in C Code
The Tree Class

• class Tree
• private
• Node pRoot
• public
• //constructor
• Tree()pRootNULL

19
Inserting node in C code
//insert node void insert(int d, float t) Node
pNewnodenew Node(d,t) if (pRootNULL) pRootpNe
wnode else Node pCurrentpRoot Node
pParent while (true) pParentpCurrent if(dltpCur
rent-gtday) pCurrentpCurrent-gtpLeftchild if(pCu
rrentNULL) pParent-gtpLeftchildpNewnode return
else pCurrentpCurrent-gtpRightchild if(pCur
rentNULL) pParent-gtpRightchildpNewnode return

20
Finding node in C
Node find(int key) Node pCurrentpRoot while(
pCurrent-gtday!key) if(keyltpCurrent-gtday) pCur
rentpCurrent-gtpLeftchild else pCurrentpCurrent-
gtpRightchild if(pCurrentNULL) return
NULL return pCurrent
21
Finding Minimum Value in c
Node minimum() Node pCurrentpRoot Node
pLast while(pCurrent!NULL) pLastpCurrent pCu
rrentpCurrent-gtpLeftchild return pLast
22
Finding Maximum Value in c
Node maximum() Node pCurrentpRoot Node
pLast while(pCurrent!NULL) pLastpCurrent pCu
rrentpCurrent-gtpRightchild return pLast
23
Finding sum in c
void sum1(float s ) sum(s,pRoot) void
sum(float s,Node plocatRoot) if(plocatRoot!NU
LL) ssplocatRoot-gttemp sum(s,plocatRoot-gtpLeft
child) sum(s,plocatRoot-gtpRightchild)
24
Finding count in c
void count (int c ) count1(c,pRoot) void
count1(int conut,Node plocatRoot) if(plocatRoo
t!NULL) conut count1(conut,plocatRoot-gtpLeftc
hild) count1(conut,plocatRoot-gtpRightchild)

25
void main() Tree tree1 int n cingtgtn int
day1 float temp1 for(int i1iltni) cingtgtda
y1gtgttemp1 tree1.insert(day1,temp1) //Finding
a node with a given key  coutltlt"\n Enter day
number to search about" int findkey cingtgtfindke
y Node pfindtree1.find(findkey) if(pfind!NULL
) coutltlt"\n found node with key"ltlt
findkeyltlt"" pfind-gtdisplaynode() else coutltlt"c
an not find node"ltltendl
26
//minimum maximum value  Nodemintree1.minimum(
) Nodemaxtree1.maximum() coutltlt"\nthe Minimum
value int the tree is"ltltmin-gtday coutltlt"\nthe
maximum value int the tree is"ltltmax-gtday coutltlte
ndl float sum0 tree1.sum_temp(sum) coutltlt"th
e sum of tempretures"ltltsumltltendl int
count0 tree1.count_day(count) coutltlt"the count
of day"ltltcountltltendl
27
Evolution questions

• Answer the following questions for the tree shown
  below. 
• What is the path length of the path from node 20
  to node 12?
• Which node is the parent of node 35? 
•  Draw the sub-tree rooted at node 43.  
•  Traverse the tree in Preorder, Inorder and
  postorder.
• Show what would this tree look like after
• Deleting 11
• Deleting 18