Weighted graphs

1
Weighted graphs

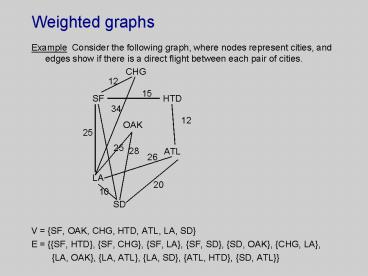
• Example Consider the following graph, where
  nodes represent cities, and edges show if there
  is a direct flight between each pair of cities.
• CHG
• SF
  HTD
• OAK
• 
  ATL
• LA
• SD
• V SF, OAK, CHG, HTD, ATL, LA, SD
• E SF, HTD, SF, CHG, SF, LA, SF, SD,
  SD, OAK, CHG, LA,
• LA, OAK, LA, ATL, LA, SD, ATL,
  HTD, SD, ATL

12
15
34
12
25
25
28
26
20
10
2

• Problem formulation find the "best" path between
  two vertices v1, v2 ? V
• in graph G (V, E). Depending on what the "best"
  path means, we have 2
• types of problems
• The minimum spanning tree problem, where the
  "best" path means the "lowest-cost" path.
• The shortest path problem, where the "best" path
  means the "shortest" path.
• Note that here edge weights are not necessarily
  Euclidean distances. Example
• 
  
  2985 gt 1421 310, not the case
• 
  here, however.

800
2
1
200
612
410
310
5
2985
400
4
3
1421
3
The Weighted Graph ADT

• Definition A weighted graph, G, is a triple (V,
  E, W), where (V, E) is a graph,
• and W is a function from E into Z, where Z is
  a set of all positive integers.
• That is, W E ? Z.
• Additional operations (methods) on weighted
  graphs
• addEdge(v1, v2, weight) Returns G with new
  edge v1v2 added
• removeEdge(v1, v2, weight) Returns G with edge
  v1v2 removed
• edgeWeight(v1, v2) Returns the
  weight of edge v1v2

4
The minimum spanning tree problem

• Definition. A minimum spanning tree of a
  weighted graph is a collection of
• edges connecting all of the vertices such that
  the sum of the weights of the
• edges is at least as small as the sum of the
  weights of any other collection of
• edges connecting all of the vertices.
• Example Consider the following graph

2
6
3
1
1
1
1
1
2
2
1
2
5
4
4
3
2
1
4
2
1
2
5

• Property of a minimum spanning tree (MST). Given
  any division of the
• vertices of a graph into two sets, the minimum
  spanning tree contains the
• shortest of the edges connecting a vertex in one
  of the sets to a vertex in the
• other set.
• This property tells us that we can start building
  the MST by selecting any
• vertex, and always taking next the vertex which
  is closest to the vertices
• already on the tree. If more than one "closest"
  vertex exists, then we can take
• anyone of these vertices (therefore, a MST of a
  graph is not unique).
• Example Let V1 a, b, c, d , V2 e, f, ,
  m. Then, the MSP must contain
• edge fd, because W(fd) 1.
• Note that V2 consists of two types of vertices
• Fringe vertices, which are adjacent to V1.
• Unseen vertices, which are not adjacent to V1.
• Extended example to be distributed in class!

6
Generation of a MST the Prim's algorithm

• The idea Select an arbitrary vertex to start
  the tree. While there are fringe
• vertices remaining, select an edge of minimum
  weight between a tree vertex
• and a fringe vertex, and add the selected edge
  and fringe vertex to the tree.
• Algorithm MST (start, T)
• Includedstart true
  // Assume Boolean array Included tells,
• for (node 2) to NumberOfNodes // which
  vertices are already in the MST.
• Includednode false
• for (node 1) to (NumberOf Nodes - 1)
• edge FindMinEdge ()
  // Requires a loop over all of the nodes.
• Includededge.IncidentNode() true
• AddEdge(edge, MST)
• Efficiency result Prim's algorithm for
  generating a MST is O(N2), where N is
• the number of nodes in the tree. Since the number
  of edges is not important it
• is good for dense graphs.

7
Generation of a MST the Kruskal's algorithm

• The idea Add edges one at a time selecting at
  each step the shortest edge
• that does not form a cycle.
• Assume that vertices of a MST are initially
  viewed as one element sets,
• and edges are arranged in a priority queue
  according to their weights. Then,
• we remove edges from the priority queue in order
  of increasing weights and
• check if the vertices incident to that edge are
  already connected. If not, we
• connect them and this way the disconnected
  components gradually evolve into
• a tree -- the minimum spanning tree.
• Extended example to be distributed in class!

8

• Efficiency result Assume that
• The priority queue is implemented as a heap.
• The minimum spanning tree is implemented as a
  weight-balanced tree.
• The graph is implemented by means of adjacency
  lists.
• Then
• The initial formation of the priority queue of
  edges is O(NumberOfEdgeslog(NumberOfEdges))
  operation.
• The phase of removing edges from the queue and
  performing one or two operations requires also
  O(NumberOfEdgeslog(NumberOfEdges)) time.
• Therefore, the total efficiency of the Kruskal's
  algorithm is O(NumberOfEdgeslog(NumberOfEdges)).

9
The shortest-path problem

• Definition. The weight, or length, of a path v0,
  v1, v2, , vk in weighted graph
• k-1
• G (V, E, W) is ? W(vi vi1). Path v0, v1,
  v2, , vk is the shortest path from
• i 0
• v0 to vk if there is no other path from v0 to vk
  with lower weight.
• Definition. The distance from vertex x to
  vertex y (x, y ? V), denoted as
• d(x,y) is the weight of the shortest path from x
  to y.
• The problem Given x ? V, we want to find the
  shortest paths from x to any
• other vertex in V in order of increasing distance
  from x. Consider the following
• two cases
• All weights are "1". Therefore, the problem
  becomes finding a path containing the minimum
  number of edges. To solve this problem, we can
  use the breadth-first search algorithm.
• If edge weights are different, we can use the
  Dijkstra's shortest path algorithm.

10
The shortest-path problem Dijkstra's algorithm

• Extended example to be distributed in class!
• To implement Dijkstra's algorithm we need the
  following data structures
• An integer array, distance, of NumberOfNodes size
  (assuming that edge weights are integers).
• A Node array, path, of NumberOfNodes size.
• A Boolean array, included, of NumberOfNodes size.
• Given the start node, the initialization of these
  arrays is the following
• includedstart true, all other entries in
  included initialized to false.
• 0, if
  node start
• distancenode EdgeWeight(start, node)
• ?,
  if there does not exist a direct edge between
• 
  start and node
• pathnode start, if there exists an edge
  between start and node
• undefined,
  otherwise.

11
Dijkstra's algorithm (contd.)

• The iteration phase
• repeat
• find the node, j, that is at the minimum
  distance from start among those
• not yet included and make includedj
  true
• for each node, r, not yet included
• if r is connected by an edge to j, then
• if distancej EdgeWeight(j, r) lt
  distancer then
• distancer distancej
  EdgeWeight(j, r)
• pathr j // path
  contains the immediate predecessor of each node
• until includeddestination_node true
• Efficiency result. If EdgeWeight operation is
  O(1), then Dijkstra's algorithm is