Instabilities in the Forced Truncated NLS
1 / 1
Title:
Instabilities in the Forced Truncated NLS
Description:
Instabilities in the Forced Truncated NLS E. Shlizerman and V. Rom-Kedar, Weizmann Institute of Science, Israel Bh Bh The Nonlinear Shr dinger Equation –
Number of Views:58
Avg rating:3.0/5.0
Title: Instabilities in the Forced Truncated NLS
1
Instabilities in the Forced Truncated NLS E.
Shlizerman and V. Rom-Kedar, Weizmann Institute
of Science, Israel
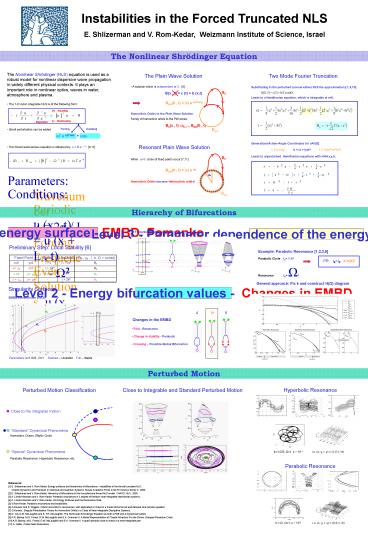
The Nonlinear Shrödinger Equation
The Nonlinear Shrödinger (NLS) equation is used
as a robust model for nonlinear dispersive wave
propagation in widely different physical
contexts. It plays an important role in nonlinear
optics, waves in water, atmosphere and plasma.
The Plain Wave Solution
Two Mode Fourier Truncation
- A solution which is independent of X. 8
Substituting in the perturbed (conservative) NLS
the approximation 7, 9,10 Leads to a
Hamiltonian equation, which is integrable at e0.
B(x , t) c (t) b (x,t)
- The 1-D cubic integrable NLS is of the following
form
Bpw(0 , t) c e i(?tf0)
() focusing
Homoclinic Orbits to the Plain Wave Solution
Family of homoclinic orbits to the PW exists
(-) de-focusing
dispersion
Bh(x , t) ?t?8 Bpw(0 , t)
- Small perturbation can be added
Forcing
Damping
ieG e i(O² t?)
ieau
- The forced autonomous equation is obtained by u
B e -i O² t 8,11
Generalized Action-Angle Coordinates for c?0 6
Resonant Plain Wave Solution
c c ei? b (x iy)ei? I
½(c2x2y2)
Leads to unperturbed Hamiltonian equations with
HH(x,y,I)
When ?0 circle of fixed points occur 7,11
Bpw(0 , t) c e if0
Parameters Wavenumber k 2p / L
Forcing Frequency O2
Homoclinic Orbits become Heteroclinic orbits!
Conditions Periodic u (x , t) u (x
L , t) Even Solutions u (x , t) u (-x , t)
Hierarchy of Bifurcations
Level 1 - Single energy surface - EMBD, Fomenko
Level 3 - Parameter dependence of the energy
bifurcation values - k, O
Fomenko Graphs (example for line 5)
Preliminary Step Local Stability 6
Example Parabolic Resonance 1,2,3,5
Fixed Point Fixed Point Stable Unstable H(xf , yf , I k, O const)
x0 y0 I gt 0 I gt ½ k2 H1
xx2 y0 I gt ½k2 - H2
x 0 yy3 I gt 2k2 - H3
x x4 yy4 - I gt 2k2 H4
Parabolic Circle Ip ½ k2
PR IRIP k22O2
Resonance IR O2
General approach Fix k and construct H(O) diagram
Singularity Surfaces
Level 2 - Energy bifurcation values - Changes in
EMBD
EMBD Construction 1,2,4
H4
4
6
5
Changes in the EMBD
H1
H3
- Fold - Resonance
H2
- Change in stability - Parabolic
- Crossing Possible Global Bifurcation
Parameters k1.025 , O1 Dashed Unstable
Full Stable
Perturbed Motion
Hyperbolic Resonance
Close to Integrable and Standard Perturbed Motion
Perturbed Motion Classification
Close to the integrable motion
Standard Dynamical Phenomena
Homoclinic Chaos, Elliptic Circle
k1.025, O1, e 10-4 i.c. (x,
y, I, ?) (1,0,1,-p)
Parabolic Resonance, Hyperbolic Resonance, etc.
Parabolic Resonance
References 1 E. Shlizerman and V. Rom-Kedar.
Energy surfaces and hierarchies of bifurcations -
instabilities in the forced truncated NLS,
Chaotic Dynamics and Transport in Classical and
Quantum Systems. Kluwer Academic Press in NATO
Science Series C, 2004. 2 E. Shlizerman and V.
Rom-Kedar. Hierarchy of bifurcations in the
truncated and forced NLS model. CHAOS,15(1),
2005. 3 A. Litvak-Hinenzon and V. Rom-Kedar.
Parabolic resonances in 3 degree of freedom
near-integrable Hamiltonian systems. 4 A.
Litvak-Hinenzon and V. Rom-Kedar. On Energy
Surfaces and the Resonance Web. 5 V.Rom-Kedar.
Parabolic resonances and instabilities. 6
G.Kovacic and S. Wiggins. Orbits homoclinic to
resonances, with application to chaos in a model
of the forced and damped sine-Gordon
equation. 7 G.Kovacic. Singular Perturbation
Theory for Homoclinic Orbits in a Class of
Near-Integrable Dissipative Systems. 8 D. Cai,
D.W. McLaughlin and K. T.R. McLaughlin. The
NonLinear Schrodinger Equation as both a PDE and
a Dynamical system. 9 A.R. Bishop, M.G. Forest,
D.W. McLaughlin and E.A. Overman II. A Modal
Representation of Chaotic Attractors For the
Driven, Damped Pendulum Chain. 10 A.R. Bishop,
M.G. Forest, D.W. McLaughlin and E.A. Overman II.
A quasi-periodic route to chaos in a
near-integrable pde. 11 G. Haller. Chaos Near
Resonance.
k v2, O1, e 10-4 i.c. (x,
y, I, ?) (0,0,1,-p)