Adding and Subtracting Polynomials - PowerPoint PPT Presentation
1 / 97
Title:
Adding and Subtracting Polynomials
Description:
Sample: monopoly, biathlon, tripod, polychrome c. yes 43. x4 + x3 + 15x 44. 7g8 2g3 11g2 + 2g 9-1 ALGEBRA 1 LESSON 9-1 45. h10 ... – PowerPoint PPT presentation
Number of Views:1324
Avg rating:3.0/5.0
Title: Adding and Subtracting Polynomials
1
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
(For help, go to Lesson 1-7.)
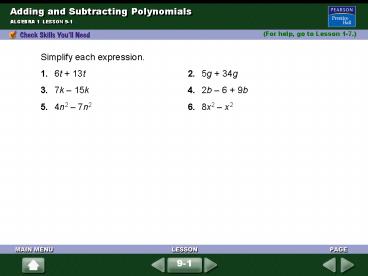
Simplify each expression. 1. 6t 13t 2. 5g
34g 3. 7k 15k 4. 2b 6 9b 5. 4n2
7n2 6. 8x2 x2
9-1
2
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
1. 6t 13t (6 13)t 19t 2. 5g 34g (5
34)g 39g 3. 7k 15k (7 15)k 8k 4. 2b
6 9b (2 9)b 6 11b 6 5. 4n2 7n2
(4 7)n2 3n2 6. 8x2 x2 (8 1)x2 7x2
Solutions
9-1
3
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
Find the degree of each monomial.
a. 18
b. 3xy3
c. 6c
9-1
4
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
Write each polynomial in standard form. Then
name each polynomial by its degree and the number
of its terms.
a. 2 7x
linear binomial
b. 3x5 2 2x5 7x
fifth degree trinomial
9-1
5
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
Simplify (6x2 3x 7) (2x2 6x 4).
Method 1 Add vertically.
Line up like terms. Then add the coefficients.
Method 2 Add horizontally.
8x2 3x 3
9-1
6
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
Simplify (2x3 4x2 6) (5x3 2x 2).
Method 1 Subtract vertically.
Line up like terms. Then add the coefficients.
9-1
7
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
(continued)
Method 2 Subtract horizontally.
(2x3 4x2 6) (5x3 2x 2)
2x3 4x2 6 5x3 2x 2 Write the opposite
of each term in the polynomial being subtracted.
9-1
8
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
pages 459461 Exercises 1. 1 2. 3 3. 0 4. 1
0 5. 4 6. 0 7. 4 8. 0 9. quadratic
trinomial 10. linear binomial 11. cubic
trinomial
21. 8m2 15 22. 10k 4 23. 8w2 3w
4 24. 20x2 7 25. 10g4 11g 26. 6a2 7a
21 27. 8y4 7y3 4y 28. 2c 14 29. b
1 30. 4h2 6h 18
12. not a polynomial 13. constant
monomial 14. quadratic binomial 15. 3x2 4x
quadratic binomial 16. 4x 9 linear
binomial 17. c2 4c 2 quadratic
trinomial 18. 2z2 5z 5 quadratic
trinomial 19. 15y8 7y3 y eighth degree
trinomial 20. 4q4 3q2 8q 10 fourth
degree polynomial with 4 terms
9-1
9
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
31. 7n4 n3 32. 15x5 x 33. 5w2 4w
10 34. 5x4 x3 7x2 x 35. 18y2
5y 36. 6x3 3x2 4 37. 7z3 6z2 2z
5 38. 7a3 11a2 4a 4 39. 28c 16 40. 39x
7 41. Kwan did not take the opposite of each
term in the polynomial being subtracted.
42. a. monogram a design composed of one or
more letters, typically the initials of a
name used as an identifying mark binocular
relating to, used by, or involving both eyes
at the same time tricuspid having three cusps,
usually said of a molar tooth polyglot a
person with a speaking, reading, or writing
knowledge of several languages b. Answers may
vary. Sample monopoly, biathlon, tripod,
polychrome c. yes 43. x4 x3 15x 44. 7g8
2g3 11g2 2g
9-1
10
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
55. a. p(t) 57t 2332.3 b. 2,617,300 c. the
difference between the number of men and the
number of women enrolled in a
college 56. D 57. G 58. A 59. C 60. B 61. C 62
. 2 (9x3 4x2 1) (x2 2) 9x3 4x2
1 x2 2 (9x3) (4x2 x2 ) (1 2)
9x3 5x2 1 1 one incorrect term OR no
work shown
45. h10 5h9 8h5 2h4 46. t4 4t
6 47. 5b9 3b8 4b7 8b 48. 5k4 k3 k2
11 49. 5x 18 50. 9a 6 51. No both terms of
a binomial cannot be constants. 52. a. y 2x
1 y 0.5x 3 b. D(x) 1.5x 4 c. or
2 d. The lines intersect at x 2 . 53. 5a3b
5ab 54. p4q4 11p4q 14pq6
8 3
2 3
2 3
9-1
11
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
63. 2 64. 1.4 65. 5 66. 5 67. exponential
growth 68. exponential decay 69. exponential
growth 70. exponential decay 71. 718 72. 21 73
. 36x5 74. 3a3b2
75. 30t7 76. (3)2 77. 12h10 78. 10q7 79. y
x 5 80. y x 6 81. y x
12 82. y x 7 83. y x 10 84. y x
0.4 85. y x 5.2 86. y x 2.3
9-1
12
Adding and Subtracting Polynomials
ALGEBRA 1 LESSON 9-1
Simplify each expression. Then name each
polynomial by its degree and number of
terms. 1. 4 3x 2x2 2. 2b2 4b3
6 3. (2x4 3x 4) (3x 4 x4) 4. (3r
4r2 3) (4r2 6r 2)
2x2 3x 4 quadratic trinomial
4b3 2b2 6 cubic trinomial
3x4 fourth degree monomial
9r 1 linear binomial
9-1
13
Multiplying and Factoring
ALGEBRA 1 LESSON 9-2
(For help, go to Lesson 17.)
Multiply. 1. 3(302) 2. 41(7) 3. 9(504) Simplify
each expression. 4. 4(6 5x) 5. 8(2y
1) 6. (5v 1)5 7. 7(p 2) 8. (6 x)9 9. 2(4q
1)
9-2
14
Multiplying and Factoring
ALGEBRA 1 LESSON 9-2
1. 3(302) 906 2. 41(7) 287 3. 9(504)
4536 4. 4(6 5x) 4(6) 4(5x) 24
20x 5. 8(2y 1) (8)(2y) (8)(1) 16y
8 6. (5v 1)5 (5v)(5) (1)(5) 25v
5 7. 7(p 2) 7p 7(2) 7p 14 8. (6 x)9
6(9) 9x 54 9x 9. 2(4q 1) (2)(4q)
(2)(1) 8q 2
Solutions
9-2
15
Multiplying and Factoring
ALGEBRA 1 LESSON 9-2
Simplify 2g2(3g3 6g 5).
2g2(3g3 6g 5)
2g2(3g3) 2g2(6g) 2g2(5) Use the
Distributive Property.
6g2 3 12g2 1 10g2 Multiply the
coefficients and add the exponents of powers with
the same base.
6g5 12g3 10g2 Simplify.
9-2
16
Multiplying and Factoring
ALGEBRA 1 LESSON 9-2
Find the GCF of 2x4 10x2 6x.
List the prime factors of each term. Identify the
factors common to all terms.
2x4 2 x x x x 10x2 2 5 x x
6x 2 3 x
The GCF is 2 x, or 2x.
9-2
17
Multiplying and Factoring
ALGEBRA 1 LESSON 9-2
Factor 4x3 12x2 16x.
Step 1 Find the GCF.
4x3 2 2 x x x 12x2 2 2 3 x
x 16x 2 2 2 2 x
4x(x2) 4x(3x) 4x(4)
4x(x2 3x 4)
The GCF is 2 2 x, or 4x.
9-2
18
Multiplying and Factoring
ALGEBRA 1 LESSON 9-2
pages 463465 Exercises 1. 8m2 48m 2. 3x2
30x 3. 63k2 36k 4. 5a2 5a 5. 18x2
2x3 6. p3 11p2 7. 12x4 2x3
10x2 8. 36y5 32y4 44y2 9. 45c5 40c4
25c3 10. 42q7 14q3 49q2 11. 3g11
18g9 15g7
12. 40x9 12x8 28x6 13. 3 14. 2a 15. 12 16.
x 17. 5 18. 3x 19. 2(3x 2) 20. v(v
4) 21. 5(2x3 5x2 4) 22. 2t2(1 5t2)
23. 3n(5n2 n 4)
24. 6p3(p3 4p2 3) 25. Karla Kevin
multiplied 2x by 3 instead of 3. 26. Answers
may vary. Sample 8x3 12x2 24x 4x(2x2
3x 6) 27. 12a3 15a2 27a 28. 14p5
35p3 29. 60c3 36c2 48c 30. 4y2
13y 31. x2 x 32. 12t 3 23t 2 33. a. A 16
x2 4x2 b. A 4x2(4 1)
9-2
19
Multiplying and Factoring
ALGEBRA 1 LESSON 9-2
34. 9m5(m7 4m2 9) 35. 24x(x2 4x
2) 36. 16n(n2 3n 5) 37. x2(5x2 4x
3) 38. 13ab3(1 3ab) 39. 7g 2k2(k
5g3) 40. 25 52 25 41. a. n(n 1) b. Always
the product of two consecutive integers is
always even since one of the integers is
even. 42. a. 1 2 3 4 (n 1) b. 5050
1 2
3 2
n 2
9-2
20
Multiplying and Factoring
ALGEBRA 1 LESSON 9-2
57. 58. 59. 60. 1 61. 62. 63. 4c3 64.
65. (3, 2) 66. (5, 3) 67. (1, 6)
1 5
50. 2 2x2(5x2 3x 1) the terms 5x2, 3x,
and 1 have no common factor other than
1. 1 incorrect factoring or incorrect
explanation 51. 3x2 10 52. m3 5m2 12m
6 53. 5g 2 g 54. r2 16r 16 55. t4 5t 2
9 56. 3b3 6b2 12
1 8
9-2
21
Multiplying and Factoring
ALGEBRA 1 LESSON 9-2
1. Simplify 2x2(3x2 2x 8). 2. Find the
GCF of 16b4 4b3 8b2. 3. Factor 3x3
9x2. 4. Factor 10y3 5y2 15y.
6x4 4x3 16x2
4b2
3x2(x 3)
5y(2y 3)(y 1)
9-2
22
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
(For help, go to Lesson 9-2.)
Find each product. 1. 4r(r 1) 2. 6h(h2 8h
3) 3. y2(2y3 7) Simplify. Write each answer in
standard form. 4. (x3 3x2 x) (5x2 x
1) 5. (3t3 6t 8) (5t3 7t 2)
6. w(w 1) 4w(w 7) 7. 6b(b 2) b(8b
3) 8. m(4m2 6) 3m2(m 9) 9. 3d2(d3 6)
d3(2d2 4)
9-3
23
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
1. 4r(r 1) 4r(r) 4r(1) 4r 2
4r 2. 6h(h2 8h 3) 6h(h2) 6h(8h) 6h(3)
6h3 48h2 18h 3. y2(2y3 7) y2(2y3) 7y2
2y5 7y2 4. x3 3x2 x 5. 3t3 6t 8
5x2 x 1 5t3 7t 2 x3 8x2
2x 1 8t3 t 6
Solutions
6. w(w 1) 4w(w 7) 7. 6b(b 2) b(8b
3) w(w) w(1) 4w(w) 4w(7) 6b(b)
6b(2) b(8b) b(3) w2 w 4w2 28w 6b2
12b 8b2 3b (1 4)w2 (1 28)w (6
8)b2 (12 3)b 5w2 27w 2b2 15b
9-3
24
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
Solutions (continued)
8. m(4m2 6) 3m2(m 9) m(4m2) m(6)
3m2(m) 3m2(9) 4m3 6m 3m3 27m2 (4
3)m3 27m2 6m 7m3 27m2 6m 9. 3d2(d3
6) d3(2d2 4) 3d2(d3) 3d2(6) d3(2d2)
d3(4) 3d5 18d2 2d5 4d3 (3 2)d5
4d3 18d2 d5 4d3 18d2
9-3
25
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
Simplify (2y 3)(y 2).
(2y 3)(y 2) (2y 3)(y) (2y
3)(2) Distribute 2y 3.
2y2 3y 4y 6 Now distribute y and 2.
2y2 y 6 Simplify.
9-3
26
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
Simplify (4x 2)(3x 6).
The product is 12x2 18x 12.
9-3
27
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
Find the area of the shaded region. Simplify.
area of outer rectangle (3x 2)(2x 1)
area of hole x(x 3)
area of shaded region area of outer rectangle
area of hole
(3x 2)(2x 1) x(x 3) Substitute.
6x2 3x 4x 2 x2 3x Use FOIL to
simplify (3x 2) (2x 1) and the Distributive
Property to simplify x(x 3).
9-3
28
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
Simplify the product (3x2 2x 3)(2x 7).
21x2 14x 21 Multiply by 7.
6x3 4x2 6x Multiply by 2x.
9-3
29
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
(continued)
Method 2 Multiply using the horizontal method.
The product is 6x3 17x2 8x 21.
9-3
30
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
pages 469472 Exercises 1. 30 2. 35 3. 7 4.
13 5. x2 7x 10 6. h2 7h 12 7. k2 k
42 8. a2 17a 72 9. 2x2 3x
2 10. 2y2 y 15 11. r 2 2r 24
12. 5y2 12y 32 13. x2 x 42 14. m2 15m
54 15. 4b2 10b 6 16. 8w2 42w 10 17. x2
2x 63 18. a2 16a 55 19. p2 9p
10 20. 8x 6 21. 2x2 5x 48 22. x3 5x2
35x 9 23. a3 6a2 9a 4
24. 2g 3 3g 2 6g 9 25. 3k3 19k2 33k
56 26. 9x3 15x2 3x 3 27. 2t 3 17t 2
36t 15 28. 56p3 103p2 37p 9 29. 48w3
28w2 2w 2 30. p2 p 56 31. p2 p
56 32. p3 8p2 7p 56 33. 25c2 40c
9 34. n3 11n2 3n 33 35. 15k4 3k3 10k2
2k
9-3
31
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
36. 24h3 2h2 17h 3 37. 9y4 9y3 7y2 2y
2 38. 48q3 16q2 4q 4 38. a. 2x2 12x
16 b. 12x 16 c. 10 ft by 5 ft 40. Answers may
vary. Sample (x 2)(x2 3x 4) x3 5x2
10x 8 41. Answers may vary. Sample
vertical method, so you can keep terms
aligned 42. 7.5x 15 43. 1.5x2 2.5x 1
44. a. x2 2x 1, 121 x2 3x 2, 132 x2
4x 3, 143 b. For ax2 bx c, a corresponds
to the hundreds place, b to the tens place,
and c to the ones place. 45. n3 15n2
56n 46. n2 6n 8 47. 6x2 36x 54 48. 96t
2 48t 6 49. 24w 4 168w 2 294 50. a. V(t)
7.02t 2 1098.6t 40,920 b. 46,588.5 million
lb 51. a. 2000r 3 6000r 2 6000r
2000 b. 2185.45
9-3
32
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
62. 2 8v3 2v2 3v 1 multiply each term of
(2v2 v 1) by 4v, and then multiply each
term of (2v2 v 1) by 1. Add the 6
products. 1 incorrect calculation OR incorrect
explanation 63. 4 (2n 6)(5n 2) (3n
2)(n 2) 10n2 26n 12 3n2 8n
4 7n2 18n 16 3 appropriate methods,
but with one computational error 2 incorrect
products subtracted correctly OR correct
products subtracted incorrectly 1 correct
answer, without work shown 64. 20v2
28v 65. 3c2 27c 66. 8t 3 48t 2
52. g 2 4 g 4 53. 16 k2 40 k
25 54. 9 x2 6 x 55. 1008 56. 4611 57. 5
824 58. 2432 59. A 60. H 61. B
9-3
33
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
67. 3y2 10y 68. 5x3 55x2 69. 6t4
t3 70. 4r6 12r 71. 9b5 18b3 72. 5(w
9) 73. x(3x 11) 74. 4a(a 3) 75. n2(9
n) 76. 17(2t 3) 77. 9v(7v 5) 78. 5m(5
12m2)
79. 11k(1 7k5) 80. 27 81. 82. y4 83. 84.
85. 86. 87. 1 88. 89. 64y4
1 27
3 5
9 25
9-3
34
Multiplying Binomials
ALGEBRA 1 LESSON 9-3
Simplify each product using any method. 1. (x
3)(x 6) 2. (2b 4)(3b 5) 3. (3x 4)(3x2
x 2) 4. Find the area of the shaded region.
x2 3x 18
6b2 22b 20
9x3 9x2 2x 8
2x2 3x 1
9-3
35
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
(For help, go to Lessons 84 and 9-3.)
Simplify. 1. (7x)2 2. (3v)2 3. (4c)2 4. (5g3)2 U
se FOIL to find each product. 5. (j 5)(j
7) 6. (2b 6)(3b 8) 7. (4y 1)(5y
2) 8. (x 3)(x 4) 9. (8c2 2)(c2
10) 10. (6y2 3)(9y2 1)
9-4
36
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
1. (7x)2 72 x2 49x2 2. (3v)2 32 v2
9v2 3. (4c)2 (4)2 c2 16c2 4. (5g3)2 52
(g3)2 25g6
Solutions
5. (j 5)(j 7) (j)(j) (j)(7) (5)(j)
(5)(7) j2 7j 5j 35 j2 12j 35
6. (2b 6)(3b 8) (2b)(3b) (2b)(8)
(6)(3b) (6)(8) 6b2 16b 18b 48
6b2 34b 48
9-4
37
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
Solutions (continued)
7. (4y 1)(5y 2)) (4y)(5y) (4y)(2)
(1)(5y) (1)(2) 20y2 8y 5y 2 20y2
3y 2
8. (x 3)(x 4) (x)(x) (x)(-4) (3)(x)
(3)(4) x2 4x 3x 12 x2 x 12
9. (8c2 2)(c2 10) (8c2)(c2) (8c2)(10)
(2)(c2) (2)(10) 8c4 80c2 2c2 20
8c4 78c2 20
10. (6y2 3)(9y2 1) (6y2)(9y2) (6y2)(1)
(3)(9y2) (3)(1) 54y4 6y2 27y2 3
54y4 21y2 3
9-4
38
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
a. Find (y 11)2.
(y 11)2 y2 2y(11) 72 Square the binomial.
y2 22y 121 Simplify.
b. Find (3w 6)2.
(3w 6)2 (3w)2 2(3w)(6) 62 Square the
binomial.
9w2 36w 36 Simplify.
9-4
39
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
Among guinea pigs, the black fur gene (B) is
dominant and the white fur gene (W) is recessive.
This means that a guinea pig with at least one
dominant gene (BB or BW) will have black fur. A
guinea pig with two recessive genes (WW) will
have white fur.
9-4
40
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
(continued)
9-4
41
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
a. Find 812 using mental math.
812 (80 1)2
b. Find 592 using mental math.
592 (60 1)2
602 2(60 1) 12 Square the binomial.
3600 120 1 3481 Simplify.
9-4
42
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
Find (p4 8)(p4 8).
(p4 8)(p4 8) (p4)2 (8)2 Find the
difference of squares.
p8 64 Simplify.
9-4
43
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
Find 43 37.
43 37 (40 3)(40 3) Express each factor
using 40 and 3.
402 32 Find the difference of squares.
1600 9 1591 Simplify.
9-4
44
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
pages 477479 Exercises 1. c2 2c 1 2. x2
8x 16 3. 4v2 44v 121 4. 9m2 42m
49 5. w 2 24w 144 6. b2 10b
25 7. 36x2 96x 64 8. 81j 2 36j
4 9. a. C2 CD D2 b. c. It
is the coefficient of C2.
10. 3721 11. 9801 12. 2304 13. 91,204 14. 249,00
1 15. x2 16 16. a2 64 17. d 2 49 18. h2
225 19. y2 144 20. k2 25 21. 899
22. 8099 23. 2496 24. 39,991 25. 89,999 26. (6x
9) units2 27. (10x 15) units2 28. x2 6xy
9y2 29. 25p2 10pq q2 30. 36m2 12mn
n2 31. x2 14xy 49y2 32. 16k2 56kj 49j
2 33. 4y2 36xy 81x2
1 16
3 8
9 16
1 16
9-4
45
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
34. 9w 2 60wt 100t 2 35. 36a2 132ab
121b2 36. 25p2 60pq 36q 2 37. 36h2 96hp
64p2 38. y10 18x4y5 81x8 39. 64k 2 64kh
16h2 40. a. R W R2 RW W
2 b. c. R W R R2 RW d. 0
41. a. b. n2 is one more than the
product (n 1)(n 1). c. The product (n 1)(n
1) is n2 1. 42. Answers may vary. Sample
(2 2)2 22 22 16 8 43. No 3
3 3 3 32 2(3)
9 3 12 9
1 2
1 2
1 2
1 2
1 4
1 4
2
1 2
/
1 2
1 2
1 2
1 2
1 2
1 2
1 2
1 2
2
1 2
1 2
2
1 2
1 2
1 4
1 2
1 4
1 2
1 2
1 2
2
/
9-4
46
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
44. 9y2 25w2 45. p2 81q2 46. 4d2
49g2 47. 49b2 64c2 48. g2 49h2 49. g6
49h4 50. 4a4 b2 51. 121x2 y6 52. 16k2
9h4 53. a2 b2 c2 2ab 2bc 2ac 54. a. H 3
H 2T HT 2 T 3 b.
4 3
1 8
3 8
3 8
1 8
3 8
3 8
9-4
47
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
58. D 59. F 60. C 61. B 62. C 63. 2 The
middle term is twice the product of the first
and last terms 2(3x)(4y)
24xy. 1 incorrect explanation 64. k2 2k
63 65. 2x2 23x 66 66. 15p2 7p 4 67. 3y2
4y 1
78. 5.23 ? 102 79. 6 ? 109 80. 7.2 ? 101
68. 24h2 8h 2 69. 72b2 74b 14 70. 2w 3
16w 2 5w 40 71. r 3 4r 2 30r
63 72. 30m5 8m3 8m 73. 8.713 ? 103 74. 3.1 ?
102 75. 6.8952 ? 104 76. 1.2 ? 106 77. 1.1 ?
101
9-4
48
Multiplying Special Cases
ALGEBRA 1 LESSON 9-4
Find each square. 1. (y 9)2 2. (2h
7)2 3. 412 4. 292 5. Find (p3 7)(p3
7). 6. Find 32 28.
y2 18y 81
4h2 28h 49
1681
841
p6 49
896
9-4
49
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
(For help, go to Skills Handbook page 721.)
List all of the factors of each
number. 1. 24 2. 12 3. 54 4. 15 5. 36 6. 56 7. 64
8. 96
9-5
50
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
1. Factors of 24 1, 2, 3, 4, 6, 8, 12,
24 2. Factors of 12 1, 2, 3, 4, 6,
12 3. Factors of 54 1, 2, 3, 6, 9, 18, 27,
54 4. Factors of 15 1, 3, 5, 15 5. Factors of
36 1, 2, 3, 4, 6, 9, 12, 18, 36 6. Factors of
56 1, 2, 4, 7, 8, 14, 28, 56 7. Factors of 64
1, 2, 4, 8, 16, 32, 64 8. Factors of 96 1, 2, 3,
4, 6, 8, 12, 16, 24, 32, 48, 96
Solutions
9-5
51
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
Factor x2 8x 15.
Find the factors of 15. Identify the pair that
has a sum of 8.
x2 8x 15 (x 3)(x 5).
9-5
52
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
Factor c2 9c 20.
Since the middle term is negative, find the
negative factors of 20.
Identify the pair that has a sum of 9.
c2 9c 20 (c 5)(c 4)
9-5
53
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
a. Factor x2 13x 48.
b. Factor n2 5n 24.
Identify the pair of factors of 48 that has a
sum of 13.
Identify the pair of factors of 24 that has a
sum of 5.
x2 13x 48 (x 16)(x 3)
n2 5n 24 (n 3)(n 8)
9-5
54
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
Factor d2 17dg 60g2.
d2 17dg 60g2 (d 3g)(d 20g)
9-5
55
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
pages 483485 Exercises 1. 5 2. 9 3. 7 4. 6
5. (r 3)(r 1) 6. (n 2)(n 1) 7. (k
3)(k 2) 8. (y 4)(y 2) 9. (x 1)(x
1) 10. (p 18)(p 1) 11. (k 14)(k 2)
12. (w 5)(w 1) 13. (m 1)(m 8) 14. (d
19)(d 2) 15. (t 7)(t 6) 16. (q 15)(q
3) 17. 5 18. 6 19. 9 20. 6 21. (x 4)(x
1) 22. (q 4)(q 2) 23. (y 5)(y 4)
24. (h 17)(h 1) 25. (x 16)(x 2) 26. (d
10)(d 4) 27. (m 2)(m 15) 28. (p 6)(p
9) 29. (p 3)(p 18) 30. A 31. B 32. B 33. (t
9v)(t 2v) 34. (x 7y)(x 5y) 35. (p
8q)(p 2q)
9-5
56
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
42. a. Factors contain the same
operation. b. Factors contain opposite
operations. 43. (k 2)(k 8) 44. (m 2)(m
12) 45. (n 4)(n 14) 46. (g 12)(g
8) 47. (x 5)(x 13) 48. (t 3)(t
25) 49. (x 14)(x 3) 50. (k 21)(k
2) 51. (m 3)(m 17) 52. (x 25y)(x 4y)
36. (m 9n)(m 6n) 37. (h 17j)(h
j) 38. (x 13y)(x 3y) 3941. Answers may
vary. Samples are given. 39. 18 (x 6)(x
3) 28 (x 7)(x 4) 10 (x 5)(x
2) 40. 12 (x 4)(x 3) 2 (x 2)(x
1) 20 (x 5)(x 4) 41. 7 (x 4)(x
3) 8 (x 6)(x 2) 13 (x 12)(x 1)
9-5
57
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
53. (t 15)(t 5) 54. (d 16e)(d
3e) 55. 4x2 12x 5 (2x 1)(2x 5) 56. 6x2
13x 6 (3x 2)(2x 3) 57. a. The signs of a
and b must be opposite. b. Since the middle
term is negative, the number with the
larger absolute value must be negative.
Therefore, a must be a negative
integer. 58. a. The signs of a and b must be
opposite.
b. Since the middle term is positive, the
number with the larger absolute value
must be positive. Therefore, b is a
negative integer. 59. (x6 7)(x6
5) 60. (t4 8)(t4 3) 61. (r 3 16)(r 3
5) 62. (m5 17)(m5 1) 63. (x6 24)(x6
5) 64. (p3 4)(p3 18) 65. B 66. F 67. D
9-5
58
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
75. 4q 2 28q 49 76. 64v 2 4 77. 9a2 54a
81 78. 9a2 25 79. 36t 2 108t 81 80. 4x2
64y 2 81. 6 weeks 82. 7, 35 83. a. 81 basic
players, 48 deluxe players b. 9719.19
68. I 69. A 70. F 71. 2 Find a pair of factors
of 40 that has a sum of 18 20 and 2.
x2 18x 40 (x 20)(x
2) 1 correct explanation with incorrect
factoring OR incorrect explanation with
correct factoring 72. x2 8x 16 73. w 2 12w
36 74. r 2 25
84. 85. 86.
9-5
59
Factoring Trinomials of the Type x2 bx c
ALGEBRA 1 LESSON 9-5
Factor each expression. 1. c2 6c 9 2. x2
11x 18 3. g2 2g 24 4. y2 y 110 5. m2
2mn n2
(c 3)(c 3)
(x 2)(x 9)
(g 6)(g 4)
(y 11)(y 10)
(m n)(m n)
9-5
60
Factoring Trinomials of the Type ax2 bx c
ALGEBRA 1 LESSON 9-6
(For help, go to Lessons 9-2 and 9-5.)
Find the greatest common factor. 1. 12x2
6x 2. 28m2 35m 14 3. 4v3 36v2 10 Factor
each expression. 4. x2 5x 4 5. y2 3y
28 6. t2 11t 30
9-6
61
Factoring Trinomials of the Type ax2 bx c
ALGEBRA 1 LESSON 9-6
1. 12x2 6x12x2 2 2 3 x x 6x 2
3 xGCF 2 3 x 6x 2. 28m2 35m
1428m2 2 2 7 m m 35m 5 7 m 14
2 7 GCF 7 3. 4v3 36v2 104v3 2 2
v v v 36v2 2 2 3 3 v v 10
2 5 GCF 2 4. Factors of 4 with a sum of 5 1
and 4x2 5x 4 (x 1)(x 4) 5. Factors of
28 with a sum of 3 4 and 7y2 3y 28 (y
4)(y 7) 6. Factors of 30 with a sum of 11
5 and 6t2 11t 30 (t 5)(t 6)
Solutions
9-6
62
Factoring Trinomials of the Type ax2 bx c
ALGEBRA 1 LESSON 9-6
Factor 20x2 17x 3.
2 10 2 3 1 10 16 1 3 2 1 3 10
32 3 1
9-6
63
Factoring Trinomials of the Type ax2 bx c
ALGEBRA 1 LESSON 9-6
Factor 3n2 7n 6.
3n2 7n 6
(1)(3) (1)(6) (1)(3) 3 (1)(6)
(1)(1) (6)(3) 17 (6)(1)
(1)(3) (2)(3) 3 (2)(3)
9-6
64
Factoring Trinomials of the Type ax2 bx c
ALGEBRA 1 LESSON 9-6
Factor 18x2 33x 30 completely.
18x2 33x 30 3(6x2 11x 10) Factor out
the GCF.
9-6
65
Factoring Trinomials of the Type ax2 bx c
ALGEBRA 1 LESSON 9-6
pages 487489 Exercises 1. (2n 1)(n
7) 2. (7d 1)(d 7) 3. (11w 3)(w
1) 4. (3x 2)(x 5) 5. (3t 11)(2t
1) 6. (3d 5)(d 4) 7. (2m 1)(8m
9) 8. (p 1)(15p 11) 9. (2y 1)(4y
13) 10. (2y 1)(y 17) 11. (x 3)(7x 9)
12. (4x 3)(2x 3) 13. (2t 3)(t 1) 14. (4y
1)(2y 3) 15. (2q 3)(q 7) 16. (7x 1)(x
3) 17. (13p 5)(p 1) 18. (5k 7)(k
1) 19. (5w 8)(2w 1) 20. (4d 5)(3d
4) 21. (7n 15)(2n 1) 22. 8(3m 1)(m
1) 23. 7(3v 7)(v 1)
24. 2(3t 4)(t 3) 25. 5(5x 3)(x
1) 26. 11(p 1)(p 6) 27. 2(4v 3)(3v
1) 28. Answers may vary. Sample 41 (4g 1)(g
10) 14 (4g 10)(g 1) 22 (2g 1)(2g
10) 29. Answers may vary. Sample 18 (5m
4)(3m 6) 54 (5m 2)(3m 12) 117 (5m
1)(3m 24) 30. Answers may vary. Sample 8
(7g 4)(5g 4) 559 (35g 1)(g 16) 46 (7g
2)(5g 8)
9-6
66
Factoring Trinomials of the Type ax2 bx c
ALGEBRA 1 LESSON 9-6
36. 28(m 1)(m 2) 37. 3(7h 4)(h
4) 38. (11n 6)(5n 2) 39. 2(6y 1)(3y
10) 40. (9w 5)(7w 6) 41. (9q 1)(11q
9) 42. 2 43. Answers may vary. Sample 5x2
12x 4 (5x 2)(x 2) 9x2 12x 3 3(3x
1)(x 1) 16x2 12x 2 2(4x 1)(2x
1) 44. x(8x 5)(7x 1) 45. (7p 3q)(7p 12q)
31. a. (2x 2)(x 2) (x 1)(2x 4) b. 2x2
6x 4 2x2 6x 4 yes c. Answers may vary.
Sample Neither factoring is complete. Each
one has a common factor, 2. 32. Answers may vary.
Sample Factor out the GCF, 2, first. Look at
the factors of 25 and 8 to find a combination
that will give you a sum of 45. 2(25x2 45x
8) 2(5x 1)(5x 8). 33. (9p 4)(6p
7) 34. 3(11r 4)(2r 1) 35. (7x 2)(2x 7)
9-6
67
Factoring Trinomials of the Type ax2 bx c
ALGEBRA 1 LESSON 9-6
54. (y 7)(y 1) 55. (t 4)(t 3) 56. (p
5)(p 4) 57. (m 3)(m 12) 58. (k 18)(k
2) 59. (g 9)(g 8) 60. (h 16)(h
3) 61. (x 15)(x 2) 62. (d 4)(d
14) 63. 7921 64. 160,801 65. 815,409
46. 54h(2g 1)(g 1) 47. a. 2 and 3 b. (x
2)(x 3) c. Answers may vary. Sample Each
x-intercept is the opposite of the last term
in a binomial factor. 48. D 49. G 50. D 51. H
52. D 53. 2 3x2 40x 75 (3x 5)(x
15) 1 one computational error OR no work
shown
9-6
68
Factoring Trinomials of the Type ax2 bx c
ALGEBRA 1 LESSON 9-6
66. 38,809 67. 1599 68. 1596 69. 39,996 70. 4891
71. , 4, 16 72. , 3, 27 73. ,
, 3 74. 5000, 5, or 75. , ,
2 76. 1000, 8, 0.32
77. 78. 79.
80.
1 2
1 9
1 81
1 3
1 20
5 100
1 10
1 1250
1 2
9-6
69
Factoring Trinomials of the Type ax2 bx c
ALGEBRA 1 LESSON 9-6
Factor each expression. 1. 3x2 14x
11 2. 6t2 13t 63 3. 9y2 48y 36
(x 1)(3x 11)
(2t 9)(3t 7)
3(3y 2)(y 6)
9-6
70
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
(For help, go to Lessons 84 and 9-4.)
Simplify each expression. 1. (3x)2 2. (5y)2 3. (15
h2)2 4. (2ab2)2
Simplify each product. 5. (c 6)(c 6) 6. (p
11)(p 11) 7. (4d 7)(4d 7)
9-7
71
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
Solutions
1. (3x)2 32 x2 9x2 2. (5y)2 52 y2
25y2 3. (15h2)2 152 (h2)2 225h4 4. (2ab2)2
22 a2 (b2)2 4a2b4 5. (c 6)(c 6) is
the difference of squares.(c 6)(c 6) c2
62 c2 36 6. (p 11)(p 11) is the square of
a binomial.(p 11)2 p2 2p(11) 112 p2
22p 121 7. (4d 7)(4d 7) is the square of a
binomial.(4d 7)2 (4d)2 2(4d)(7) 72
16d2 56d 49
9-7
72
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
Factor m2 6m 9.
m2 6m 9 m m 6m 3 3 Rewrite first
and last terms.
m m 2(m 3) 3 3 Does the middle term
equal 2ab? 6m 2(m 3)
(m 3)2 Write the factors as the square of a
binomial.
9-7
73
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
The area of a square is (16h2 40h 25) in.2.
Find the length of a side.
16h2 40h 25 (4h)2 40h 52 Write 16h2 as
(4h)2 and 25 as 52.
(4h 5)2 Write the factors as the square of a
binomial.
The side of the square has a length of (4h 5)
in.
9-7
74
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
Factor a2 16.
a2 16 a2 42 Rewrite 16 as 42.
(a 4)(a 4) Factor.
9-7
75
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
Factor 9b2 25.
9b2 225 (3b)2 52 Rewrite 9b2 as (3b)2 and
25 as 52.
(3b 5)(3b 5) Factor.
9-7
76
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
Factor 5x2 80.
5x2 80 5(x2 16) Factor out the GCF of 5.
5(x 4)(x 4) Factor (x2 16).
9-7
77
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
pages 493495 Exercises 1. (c 5)2 2. (x
1)2 3. (h 6)2 4. (m 12)2 5. (k
8)2 6. (t 7)2 7. (2m 5) 8. (7d
2) 9. (5g 4) 10. (5g 3)2 11. (8r 9)2
12. (10v 11)2 13. (x 2)(x 2) 14. (y 9)(y
9) 15. (k 14)(k 14) 16. (r 12)(r
12) 17. (h 10)(h 10) 18. (m 15)(m
15) 19. (w 16)(w 16) 20. (x 20)(x
20) 21. (y 30)(y 30) 22. (5q 3)(5q
3) 23. (7y 2)(7y 2)
24. (3c 8)(3c 8) 25. (2m 9)(2m
9) 26. (4k 7)(4k 7) 27. (12p 1)(12p
1) 28. (9v 10)(9v 10) 29. (20n 11)(20n
11) 30. (5w 14)(5w 14) 31. 3(m 2)(m
2) 32. 5(k 7)(k 7) 33. 3(x 8)2 34. 2(t
9)2 35. 6r (r 5)(r 5)
9-7
78
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
44. a. Answers may vary. Sample 4x2 24x
36 b. because (2x)2 4x2, 2(2x 6) 24x,
and 62 36 45. 25(2v w)(2v w) 46. 4(2p
3q)2 47. 7(2c 5d)2 48. m m
49. x 50. 16(2g 3h)2 51. p 2
36. 7(h 4)2 37. Answers may vary. Sample
Rewrite the first and last terms as a square.
Check to see if the middle term is 2ab. Factor
as a square binomial 4x2 12x 9 (2x)2
12x 32 (2x)2 2(2x)(3) 32 (2x 3)2
9x2 30x 25 (3x)2 30x 52 (3x)2
2(3x)(5) 52 (3x 5)2. 38. 4x2 121 is the
difference of two squares. So the answer should
be (2x 11)(2x 11). 39. 11, 9 40. 13,
7 41. 15, 5 42. 13, 9 43. 16, 14
1 2
1 3
1 2
1 3
1 2
2
2
1 2
9-7
79
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
52. n n 53. k
3 54. a. 3.14n2 3.14m2 3.14(n m)(n
m) b. 285.74 in.2 55. a. 4(x 5)(x 5) b. 4(x
5)(x 5) c. The polynomial has a GCF that
has two identical factors. d. 3(x 5)(x
5) no, because 3 does not have a pair of
identical factors.
56. (8r 3 9)2 57. (p3 20q)2 58. (6m2
7)2 59. (9p5 11)2 60. 3(6m3 7)(6m3
7) 61. (x10 2y5)2 62. 4(8g 2 5h3)(8g 2
5h3) 63. 5(3x2 2y)2 64. 37(g4 h4)(g 2
h2)(g h)(g h) 65. a. t 3 4 b. (t 1)(t
7)
1 3
1 5
1 3
1 5
1 5
2
9-7
80
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
75. (2t 1)(2t 7) 76. (5w 1)(w 9) 77. (3t
8)(2t 1) 78. (7m 9)(3m 1) 79. (7x
9)(2x 1) 80. (2y 11)(2y 5) 81. (3k 2)(4k
1) 82. 768 3072 12,288 3 4n-1 83. 29 37
45 11 8n 84. 11 20 29 34
9n 85. 0.02 0.002 0.0002 2000
n 86. 32 64 128 (2)n
66. a. (4 9n2)(2 3n)(2 3n) b. They are
squares of square terms. c. Answers may vary.
Sample 16x4 1 67. 9 68. 12 69. 30 70. 5
71. 12 72. 2.5 73. (2d 1)(d 5) 74. (2x
3)(x 4)
1 10
9-7
81
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
9-7
82
Factoring Special Cases
ALGEBRA 1 LESSON 9-7
Factor each expression. 1. y2 18y 81 2. 9a2
24a 16 3. p2 169 4. 36x2 225 5. 5m2
45 6. 2c2 20c 50
(y 9)2
(3a 4)2
(p 13)(p 13)
(6x 15)(6x 15)
5(m 3)(m 3)
2(c 5)2
9-7
83
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
(For help, go to Lessons 9-2 and 9-3.)
Find the GCF of the terms of each
polynomial. 1. 6y2 12y 4 2. 9r3 15r2
21r 3. 30h3 25h2 40h 4. 16m3 12m2
36m Find each product. 5. (v 3)(v2
5) 6. (2q2 4)(q 5) 7. (2t 5)(3t 4) 8. (4x
1)(x2 2x 3)
9-8
84
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
1. 6y2 12y 4 2. 9r3 15r2 21r 6y2 2
3 y y 9r3 3 3 r r r 12y 2
2 3 y 4 2 2 15r2 3 5 r r 21r
3 7 r GCF 2 GCF 3r 3. 30h3 25h2
40h 4. 16m3 12m2 36m 30h3 2 3 5 h
h h 16m3 2 2 2 2 m m m 25h2
5 5 h h 12m2 2 2 3 m m 40h
2 2 2 5 h 36m 2 2 3 3 m GCF
5h GCF 2 2 m 4m
Solutions
5. (v 3)(v2 5) (v)(v2) (v)(5) (3)(v2)
(3)(5) v3 5v 3v2 15 v3 3v2 5v
15
9-8
85
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
Solutions (continued)
6. (2q2 4)(q 5) (2q2)(q) (2q2)(5)
(4)(q) (4)(5) 2q3 10q2 4q 20
7. (2t 5)(3t 4) (2t)(3t) (2t)(4)
(5)(3t) (5)(4) 6t2 8t 15t 20 6t2
7t 20
8. (4x 1)(x2 2x 3) (4x)(x2) (4x)(2x)
(4x)(3) (1)(x2) (1)(2x) (1)(3) 4x3
8x2 12x x2 2x 3 4x3 (8 1)x2
(12 2)x 3 4x3 7x2 10x 3
9-8
86
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
Factor 6x3 3x2 4x 2.
6x3 3x2 4x 2 3x2(2x 1) 2(2x
1) Factor the GCF from each group of two terms.
(2x 1)(3x2 2) Factor out (2x 1).
9-8
87
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
Factor 8t4 12t3 16t 24.
8t4 12t3 16t 24 4(2t4 3t3 4t
6) Factor out the GCF, 4.
4t3(2t 3) 2(2t 3) Factor by grouping.
4(2t 3)(t3 2) Factor again.
9-8
88
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
Factor 24h2 10h 6.
Step 1 24h2 10h 6 2(12h2 5h
3) Factor out the GCF, 2.
Step 2 12 3 36 Find the product ac.
Step 4 12h2 4h 9h 3 Rewrite the trinomial.
Step 5 4h(3h 1) 3(3h 1) Factor by
grouping. (4h 3)(3h 1) Factor again.
24h2 10h 6 2(4h 3)(3h 1) Include the
GCF in your final answer.
9-8
89
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
A rectangular prism has a volume of 36x3 51x2
18x. Factor to find the possible expressions
for the length, width, and height of the prism.
Factor 36x3 51x2 18x.
Step 1 3x(12x2 17x 6) Factor out the GCF, 3x.
Step 2 12 6 72 Find the product ac.
9-8
90
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
(continued)
Step 4 3x(12x2 8x 9x 6) Rewrite the
trinomial.
Step 5 3x4x(3x 2) 3(3x 2) Factor by
grouping.
3x(4x 3)(3x 2) Factor again.
The possible dimensions of the prism are 3x, (4x
3), and (3x 2).
9-8
91
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
pages 499501 Exercises 1. 2m2 3 2. 5p2
2 3. 2z2 5 4. 3n2 1 5. (2n2 1)(3n
4) 6. (7t 2 8)(2t 3) 7. (3t 1)(3t 1)(3t
5) 8. (y2 1)(13y 8) 9. (5x2 1)(9x
4) 10. (2w2 3)(5w 8) 11. 2(2v2 1)(3v
8) 12. q(q 2 4)(7q 4) 13. 2(m2 2)(10m
9)
27. 5k, (k 2), and (k 4) 28. 7h(h 6)(h
1) 29. 2(10t 2 11)(3t 10) 30. 8(d 2 3)(d
2) 31. 4(3x 7y)(x 2y) 32. 9r (3r 1)(2r
1) 33. 10(5k2 6)(3k 7) 34. a. (7x2 9)(4x
1) b. (4x 1)(7x2 9) c. Answers may vary.
Sample The factorings are equivalent but
the factors may appear in a different order.
14. 2x(x 1)(x 1)(3x 2) 15. 2(2y2 5)(3y
5) 16. 3(c2 2)(3c 4) 17. (6p 5)(2p
1) 18. (4t 3)2 19. (6n 1)(3n 10) 20. (3w
5)(3w 4) 21. 2(6m 1)(2m 1) 22. (12v
7)(3v 1) 23. (3x 2)(2x 5) 24. (4v 1)(5v
9) 25. (7q 2)(9q 10) 26. m, (3m 1), and
(m 2)
9-8
92
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
44. (h 2)(h 2)(h 11) 45. (w 2 3)(w 2
3)(w 1)(w 1) 46. a. 2 x(x 3)2 b. x
3 47. (23 20)(22 21 20) (9)(7) 48. (24
22 20) (21 20) (21)(3) 49. Answers may vary.
Samples are given. a. length 2x 4 width
x height x 4 b. 2x3 12x2
16x 50. C 51. H 52. 2 9a4 54a3 2a 12
9a3(a 6) 2(a 6) (9a3 2)(a
6) 1 appropriate methods with one
computational error
35. (7w 2 4)(2w 7) 36. (2m2 1)(m
16) 37. 2(2t 2 3)(11t 1) 38. (x2 2)(25x
1) 39. 2w, (6w 5), and (7w 1) 40. Answers may
vary. Sample 30x2 36x 40x 48 2(3x
4)(5x 6) 41. Answers may vary. Sample Split
the expression into two groups. Remove the GCF
from each group, and then factor
again. 42. (6m3 7n2)(5m2 4n) 43. (x2 y)(p
q5)
9-8
93
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
72. 9 ? 1012 73. 4.9 ? 1011 74. 3.2 ?
1036 75. 2.809 ? 105 76. 6.561 ? 105 77. 6.859
? 1024 78. 6.25 ? 104 79. (1, 5) 80. (4,
8) 81. (0.5, 5) 82. (2, 30) 83. infinitely
many solutions on the liney 4x 25 84. (7,
2)
53. 4 96x3 48x2 6x 6x(16x2 8x 1)
6x(4x 1)2. Side of square equals 4x 1.
Perimeter 4(4x 1) 16x
4. 3 appropriate methods, but with one
computational error 2 found factors of
polynomial, but did not find
perimeter 1 correct answer, without work
shown 54. (k 7)2 55. (r 3)2 56. (y
8)2 57. 2(t 3)2
9-8
94
Factoring by Grouping
ALGEBRA 1 LESSON 9-8
Factor each expression. 1. 10p3 25p2 4p
10 2. 36x4 48x3 9x2 12x 3. 16a3 24a2
12a 18
(5p2 2)(2p 5)
3x(4x2 1)(3x 4)
2(4a2 3)(2a 3)
9-8
95
Polynomials and Factoring
ALGEBRA 1 CHAPTER 9
1. 2y2 3y 5 quadratic trinomial 2. 2v3
6v2 17v cubic trinomial 3. 8x4 6x2 10
fourth degree trinomial 4. 3k5 k2 fifth
degree binomial 5. 11x2 3x 7 6. 15a2 17a
7 7. 11m2 4m 2 8. 7c3 9c2
9c 9. Answers may vary. Sample p6 p2
1 10. x2 5x 6 (x 3)(x 2) 11. 8b3
24b2 56b 12. 5t 3 t 2
13. 9q4 3q2 12q 14. 2c6 8c4 15. x2 7x
6 16. d2 d 12 17. 2h2 9h 4 18. 6m2 m
35 19. 2p3 p2 6p 8 20. 6a3 14a2 43a
12 21. 21x3 29x2 7x 5 22. 3x2 23. t 24. 3a
5
9-A
96
Polynomials and Factoring
ALGEBRA 1 CHAPTER 9
25. m2 26. Multiply each term of the first
polynomial by each term of the second
polynomial. Then combine like terms. Example
(x 3)(x2 x 1) x3 x2 x 3x2 3x
3 x3 2x2 2x 3 27. x(3x 5)
(3x2 5x) m2 28. w(w 2)(4w 3) (4w 3 5w 2
6w) in.3 29. 4x2 3x 30. 4x2 x 31. (w
7)(w 2) 32. (g 5)2 33. (3k 4)2
34. (n 10)(n 10) 35. (y 2)2 36. (2x
7)(2x 7) 37. (2p 81)(2p 1) 38. 13(c 2)(c
2) 39. 14 40. 4 41. 25 42. 36 43. 3x3
4 44. 4n2 1 45. (3n2 1)(4n 5)
9-A
97
Polynomials and Factoring
ALGEBRA 1 CHAPTER 9
46. 2(2x 3)(x 1) 47. (x2 5)(x 5) 48. (3r
2 2)(2r 3) 49. (2y 1)(2y 1)(3y
7) 50. (n2 2)(3n 4) 51. Answers may vary.
Sample 13, (x 10)(x 3) 11, (x 5)(x
6) 31, (x 1)(x 30)
9-A