Review of Semiconductor Physics - PowerPoint PPT Presentation
Title:
Review of Semiconductor Physics
Description:
Review of Semiconductor Physics Energy bands Bonding types classroom discussion The bond picture vs. the band picture Bonding and antibonding – PowerPoint PPT presentation
Number of Views:274
Avg rating:3.0/5.0
Title: Review of Semiconductor Physics
1
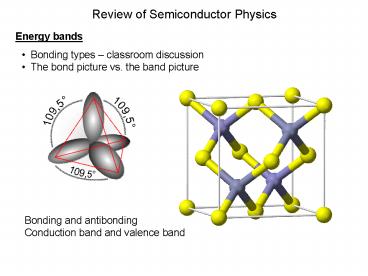
Review of Semiconductor Physics
Energy bands
- Bonding types classroom discussion
- The bond picture vs. the band picture
Bonding and antibonding Conduction band and
valence band
2
- The band picture Blochs Theorem
Notice its a theorem, not a law. Mathematically
derived.
The theorem
The eigenstates ?(r) of the one-electron
Hamiltonian
where V(r R) V(r) for all R in a Bravais
lattice, can be chosen to have the form of a
plane wave times a function with the periodicity
of the Bravais lattice
where un,k(r R) un,k(r) . Equivalently,
Physical picture
- Wave function
3
Indirect gap
- Band structure
1D case
3D case
4
Direct gap
5
Limitations of the band theory
Static lattice Will introduce phonons Perfect
lattice Will introduce defects One-electron
Shrödinger Eq We in this class will live with
this
Justification the effect of other electrons can
be regarded as a kind of background.
6
Semi-classic theory
Free electron
Block electron
hk is the momentum.
hk is the crystal momentum, which is not a
momentum, but is treated as momentum in the
semiclassical theory. n is the band index.
En(k) En(kK)
1D
3D
1D
3D
un,k(r R) un,k(r)
7
The Bloch (i.e. semiclassic) electron behaves as
a particle following Newtons laws.
(We are back in the familiar territory.)
- With a mass m
- Emerging from the other side of the first
Brillouin zone upon hitting a boundary
Newtons 1st law the Bloch electron moves
forever No resistance?
Newtons 2nd law
F dp/dt hdk/dt
Oscillation in dc field. So far not observed yet.
8
Real crystals are not perfect. Defects scatter
electrons.
On average, the electron is scattered once every
time period ?. Upon scattering, the electron
forgets its previous velocity, and is
thermalized.
Mobility
9
Values of k
Discrete but quasi-continuous
k 2?n/L, n 1, 2, 3, , N
L Na
Run the extra mile Show the above by using the
periodic boundary condition.
Holes
A vacancy in a band, i.e. a k-state missing the
electron, behaves like a particle with charge q.
Run the extra mile Show the above.
10
Review of Semiconductor Physics
Carrier Statistics
- Fermi-Dirac distribution
Nature prefers low energy. Lower energy states
(levels) are filled first. Imaging filling a
container w/ sands, or rice, or balls, or whatever
- Each particle is still T 0 K
- Each has some energy, keeping bouncing around T gt
0 K
- Density of States
How many states are there in the energy interval
dE at E? D(E)dE
1D case derived in class.
The take-home message D(E) ? E?1/2
11
2D case
Run the extra mile Derive D(E) in 2D. Hint count
number of ks in 2D.
The answer
Or, for unit area
D(E) constant
The take-home message
3D case
Run the extra mile Derive D(E) in 3D. Hint count
number of ks in 2D.
For unit area,
The take-home message D(E) ? E1/2
12
Things we have ignored so far degeneracies
Spin degeneracy 2 Valley degeneracy Mc Mc 6
for Si
13
Total number of carriers per volume (carrier
density, carrier concentration)
Run the extra mile Derive the electron density
n. Hint Fermi-Dirac distribution approximated by
Boltzmann distribution.
Results for n and p are given.
p is the total number of states NOT occupied.
Doping One way to manipulate carrier density is
doping. Doping shifts the Fermi level.
np ni2
14
One small thing to keep in mind Subtle
difference in jargons used by EEs and physicists
We use the EE terminology, of course.
EF EF(T)
Fermi level
Same concept
Physicists
?(T)
Chemical potential
EF ?(0)
Fermi energy
We already used ? for mobility.
15
Before we talk about device, what are
semiconductors anyway?
Classroom discussion
Why can we modulate their properties by orders of
magnitude?
Classroom discussion
16
We have mentioned defect scattering
Real crystals are not perfect. Defects scatter
electrons.
On average, the electron is scattered once every
time period ?. Upon scattering, the electron
forgets its previous velocity, and is
thermalized.
Mobility
Any deviation from perfect periodicity is a
defect. A perfect surface is a defect.
17
Phonons
Static lattice approximation
Atoms vibrate
Harmonic approximation
Vibration quantized
Each quantum is a phonon. Similar to the photon
E h?, p hk
Phonons scatter carriers, too. The higher the
temperature, the worse phonon scattering. You can
use the temperature dependence of conductivity or
mobility to determine the contributions of
various scattering mechanisms.
18
Phonons
? vk
Sound wave in continuous media
Microscopically, the solid is discrete.
Phonon dispersion
Wave vector folding, first Brillouin zone.
Watch video at http//en.wikipedia.org/wiki/FileP
honon_k_3k.gif
Recall that
Crystal structure Bravais lattice basis
If there are more than 1 atom in the basis,
optical phonons
19
Phonons in the 3D world -- Si
In 3D, there are transverse and longitudinal
waves.
E h? h?
62 meV
15 THz
When electron energy is low, the electron only
interacts with acoustic phonons,
20
Optical phonons and transport
At low fields,
38 meV
vth 2.3 107 cm/s
For Si,
At high fields, vd comparable to vth Electrons
get energy from the field, hotter than the
lattice hot electrons
When the energy of hot electrons becomes
comparable to that of optical phonons, energy is
transferred to the lattice via optical phonons.
Velocity saturation
For Si, vsat 107 cm/s
21
Alloys
Compounds, alloys, heterostructures
InP, GaAs, , SiC
InxGa1-xAsyP1-y, , SixGe1-x
Epitaxy
Band structure of alloys
22
- Topics
- Review of Semiconductor physics
- Crystal structure, band structures, band
structure modification by alloys,
heterostructurs, and strain - Carrier statistics
- Scattering, defects, phonons, mobility, transport
in heterostructures - Device concepts
- MOSFETs, MESFETs, MODFETs, TFTs
- Heterojunction bipolar transistors (HBT)
- Semiconductor processing
- Photodiodes, LEDs, semiconductor lasers
- (optional) resonant tunneling devices, quantum
interference devices, single electron
transistors, quantum dot computing, ... - Introduction to nanoelectronics
We will discuss heterostructures in the context
of devices.
More discussions on semiconductor physics will be
embedded in the device context.