7-4 Similarity in Right Triangles

1
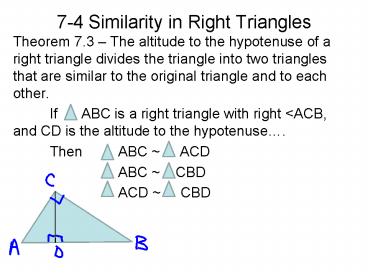
7-4 Similarity in Right Triangles

• Theorem 7.3 The altitude to the hypotenuse of a
  right triangle divides the triangle into two
  triangles that are similar to the original
  triangle and to each other.
• If ABC is a right triangle with right ltACB,
  and CD is the altitude to the hypotenuse.
• Then ABC ACD
• ABC CBD
• ACD CBD

2
7-4 Similarity in Right Triangles

• Geometric mean (between two numbers) is the
  positive square root of their product.
• For two positive numbers a and b, the geometric
  mean is the positive number x where the
  proportion ax xb is true.
• This proportion can be written using fractions as
  a/xx/b or with cross products as x2 ab or x
  ?ab
• Ex) 4 and 9 4/x x/9
• x2 36
• x ?36 or x6 ignore the negative
• answer to the square root
• Ex)6 and 15 6/xx/15
• x290 or x?90 or x 3?10 this is the
  answer that I want to see x?9.5 on calculator

3
7-4 Similarity in Right Triangles

• Corollary 1 to Theorem 7-3
• The length of the altitude to the hypotenuse of
  a right triangle is the geometric mean of the
  lengths of the segments of the hypotenuse.

4
7-4 Similarity in Right Triangles

• Corollary 2 to Theorem 7-3
• The altitude to the hypotenuse of a right
  triangle separates the hypotenuse so that the
  length of each leg of the triangle is the
  geometric mean of the length of the segment of
  the hypotenuse adjacent to the leg.