Review (2nd order tensors):

1
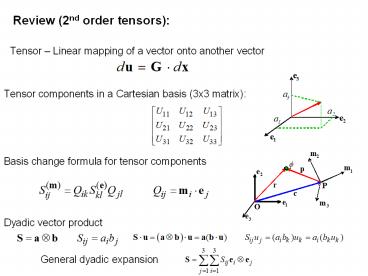
Review (2nd order tensors)
Tensor Linear mapping of a vector onto another
vector
Tensor components in a Cartesian basis (3x3
matrix)
Basis change formula for tensor components
Dyadic vector product
General dyadic expansion
2
Routine tensor operations
Addition
Vector/Tensor product
Tensor product
3
Routine tensor operations
Transpose
Trace Inner product Outer product Determinant Inv
erse Invariants (remain constant under basis
change) Eigenvalues, Eigenvectors
(Characteristic Equation Cayley-Hamilton
Theorem)
4
Recipe for computing eigenvalues of symmetric
tensor
5
Special Tensors
Symmetric tensors
Have real eigenvalues, and orthogonal eigenvectors
Skew tensors
Have dual vectors satisfying
Proper orthogonal tensors
Represent rotations have Rodriguez
representation
Polar decomposition theorem
6
Polar Coordinates
Basis change formulas
7
Gradient operator
8
Review
Deformation Mapping
Eulerian/Lagrangian descriptions of motion
Deformation Gradient
9
Review
Sequence of deformations
Lagrange Strain
10
Review
Volume Changes
Area Elements
Infinitesimal Strain
Approximates L-strain
Related to Engineering Strains
11
Review
Principal values/directions of Infinitesimal
Strain
Infinitesimal rotation
Decomposition of infinitesimal motion
12
Review
Left and Right stretch tensors, rotation tensor
U,V symmetric, so
principal stretches
Left and Right Cauchy-Green Tensors
13
Review
Generalized strain measures
Eulerian strain
14
Review
Velocity Gradient
Stretch rate and spin tensors
15
Review
Vorticity vector


Spin-acceleration-vorticity relations
16
Review Kinetics
Surface traction
Body Force
Internal Traction
Resultant force on a volume
17
Review Kinetics
Restrictions on internal traction vector
Newton II
Newton IIIII
Cauchy Stress Tensor
18
Other Stress Measures
Kirchhoff
Nominal/ 1st Piola-Kirchhoff
Material/2nd Piola-Kirchhoff
19
Review Reynolds Transport Relation
20
Review
Mass Conservation
Linear Momentum Conservation
Angular Momentum Conservation
21
Rate of mechanical work done on a material volume
Conservation laws in terms of other stresses
Mechanical work in terms of other stresses
22
Review Thermodynamics
Temperature
Specific Internal Energy Specific Helmholtz free
energy
Heat flux vector
External heat flux
Specific entropy
First Law of Thermodynamics
Second Law of Thermodynamics
23
Conservation Laws for a Control Volume
R is a fixed spatial region material flows
across boundary B
Mass Conservation
Linear Momentum Conservation
Angular Momentum Conservation
Mechanical Power Balance
First Law
Second Law
24
Review Transformations under observer changes
Transformation of space under a change of observer
All physically measurable vectors can be regarded
as connecting two points in the inertial frame
These must therefore transform like vectors
connecting two points under a change of observer
Note that time derivatives in the observers
reference frame have to account for rotation of
the reference frame
25
Some Transformations under observer changes
26
Constitutive Laws
Equations relating internal force measures to
deformation measures are knownas Constitutive
Relations

• General Assumptions
• Local homogeneity of deformation
• (a deformation gradient can always be
  calculated)
• Principle of local action
• (stress at a point depends on deformation
  in a vanishingly small material element
  surrounding the point)
• Restrictions on constitutive relations
• 1. Material Frame Indifference
  stress-strain relations must transform
  consistently under a change of observer
• 2. Constitutive law must always satisfy
  the second law of
• thermodynamics for any possible
  deformation/temperature history.