Trapezoids and Kites - PowerPoint PPT Presentation
1 / 27
Title:
Trapezoids and Kites
Description:
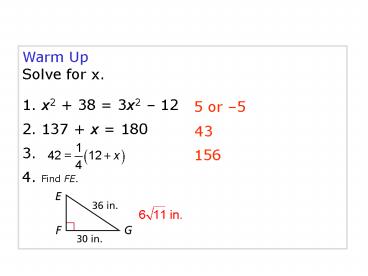
Warm Up Solve for x. 1. x2 + 38 = 3x2 12 2. 137 + x = 180 3. 4. Find FE. 5 or 5 43 156 Trapezoids and Kites 9-4 Homework Pg 473 #1-6, 13-16, 24, 28-30 ... – PowerPoint PPT presentation
Number of Views:143
Avg rating:3.0/5.0
Title: Trapezoids and Kites
1
Warm Up Solve for x. 1. x2 38 3x2 12 2.
137 x 180 3. 4. Find FE.
5 or 5
43
156
2
Trapezoids and Kites
- 9-4
3
A kite is a quadrilateral with exactly two pairs
of congruent consecutive sides.
4
A trapezoid is a quadrilateral with exactly one
pair of parallel sides. Each of the parallel
sides is called a base. The nonparallel sides are
called legs. Base angles of a trapezoid are two
consecutive angles whose common side is a base.
5
9-18
6
9-16
9-17
7
The midsegment of a trapezoid is the segment
whose endpoints are the midpoints of the legs. In
Lesson 5-1, you studied the Triangle Midsegment
Theorem. The Trapezoid Midsegment Theorem is
similar to it.
8
(No Transcript)
9
Example 1 Problem-Solving Application
Lucy is framing a kite with wooden dowels. She
uses two dowels that measure 18 cm, one dowel
that measures 30 cm, and two dowels that measure
27 cm. To complete the kite, she needs a dowel to
place along . She has a dowel that is 36 cm
long. About how much wood will she have left
after cutting the last dowel?
10
Example 1 Continued
The answer will be the amount of wood Lucy has
left after cutting the dowel.
11
Example 1 Continued
N bisects JM.
Pythagorean Thm.
Pythagorean Thm.
12
Example 1 Continued
Lucy needs to cut the dowel to be 32.4 cm long.
The amount of wood that will remain after the cut
is, 36 32.4 ? 3.6 cm Lucy will have 3.6 cm
of wood left over after the cut.
13
Example 2 Using Properties of Kites
In kite ABCD, m?DAB 54, and m?CDF
52. Find m?BCD.
Kite ? cons. sides ?
?BCD is isos.
2 ? sides ?isos. ?
isos. ? ?base ?s ?
?CBF ? ?CDF
Def. of ? ? s
m?CBF m?CDF
Polygon ? Sum Thm.
m?BCD m?CBF m?CDF 180
14
Example 2 Continued
m?BCD m?CBF m?CDF 180
Substitute m?CDF for m?CBF.
m?BCD m?CBF m?CDF 180
Substitute 52 for m?CBF.
m?BCD 52 52 180
Subtract 104 from both sides.
m?BCD 76
15
Example 3 Using Properties of Kites
In kite ABCD, m?DAB 54, and m?CDF
52. Find m?ABC.
Kite ? one pair opp. ?s ?
?ADC ? ?ABC
Def. of ? ?s
m?ADC m?ABC
Polygon ? Sum Thm.
m?ABC m?BCD m?ADC m?DAB 360
Substitute m?ABC for m?ADC.
m?ABC m?BCD m?ABC m?DAB 360
16
Example 3 Continued
m?ABC m?BCD m?ABC m?DAB 360
Substitute.
m?ABC 76 m?ABC 54 360
Simplify.
2m?ABC 230
m?ABC 115
Solve.
17
Example 4 Using Properties of Kites
In kite ABCD, m?DAB 54, and m?CDF
52. Find m?FDA.
Kite ? one pair opp. ?s ?
?CDA ? ?ABC
m?CDA m?ABC
Def. of ? ?s
? Add. Post.
m?CDF m?FDA m?ABC
52 m?FDA 115
Substitute.
Solve.
m?FDA 63
18
Example 5 Using Properties of Isosceles
Trapezoids
Find m?A.
Same-Side Int. ?s Thm.
m?C m?B 180
Substitute 100 for m?C.
100 m?B 180
Subtract 100 from both sides.
m?B 80
Isos.? trap. ?s base ?
?A ? ?B
Def. of ? ?s
m?A m?B
Substitute 80 for m?B
m?A 80
19
Example 6 Using Properties of Isosceles
Trapezoids
KB 21.9m and MF 32.7. Find FB.
Isos. ? trap. ?s base ?
Def. of ? segs.
KJ FM
Substitute 32.7 for FM.
KJ 32.7
Seg. Add. Post.
KB BJ KJ
Substitute 21.9 for KB and 32.7 for KJ.
21.9 BJ 32.7
Subtract 21.9 from both sides.
BJ 10.8
20
Example 6 Continued
Same line.
Isos. trap. ? ?s base ?
?KFJ ? ?MJF
Isos. trap. ? legs ?
SAS
?FKJ ? ?JMF
CPCTC
?BKF ? ?BMJ
Vert. ??s ?
?FBK ? ?JBM
21
Example 6 Continued
Isos. trap. ? legs ?
AAS
?FBK ? ?JBM
CPCTC
Def. of ? segs.
FB JB
Substitute 10.8 for JB.
FB 10.8
22
Check It Out! Example 7
JN 10.6, and NL 14.8. Find KM.
Isos.? trap. ?s base ?
Def. of ? segs.
KM JL
Segment Add Postulate
JL JN NL
Substitute.
KM JN NL
Substitute and simplify.
KM 10.6 14.8 25.4
23
Example 8 Applying Conditions for Isosceles
Trapezoids
Find the value of a so that PQRS is isosceles.
Trap. with pair base ?s ? ? isosc. trap.
?S ? ?P
m?S m?P
Def. of ? ?s
Substitute 2a2 54 for m?S and a2 27 for m?P.
2a2 54 a2 27
Subtract a2 from both sides and add 54 to both
sides.
a2 81
a 9 or a 9
Find the square root of both sides.
24
Example 9 Applying Conditions for Isosceles
Trapezoids
AD 12x 11, and BC 9x 2. Find the value of
x so that ABCD is isosceles.
Diags. ? ? isosc. trap.
Def. of ? segs.
AD BC
Substitute 12x 11 for AD and 9x 2 for BC.
12x 11 9x 2
Subtract 9x from both sides and add 11 to both
sides.
3x 9
Divide both sides by 3.
x 3
25
Example 10 Finding Lengths Using Midsegments
Find EF.
Trap. Midsegment Thm.
Substitute the given values.
Solve.
EF 10.75
26
Check It Out! Example 11
Find EH.
Trap. Midsegment Thm.
Substitute the given values.
Simplify.
Multiply both sides by 2.
33 25 EH
Subtract 25 from both sides.
13 EH
27
Homework
- Pg 473 1-6, 13-16, 24, 28-30