Area Of Shapes. - PowerPoint PPT Presentation
Title:
Area Of Shapes.
Description:
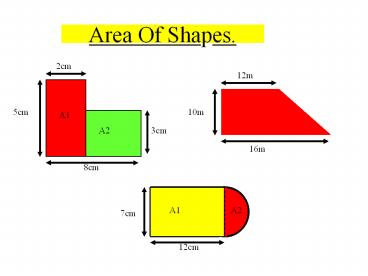
2cm Area Of Shapes. 12m A1 A2 7cm 5cm 10m A1 3cm 12cm A2 16m 8cm What Is Area ? Estimating The Area. Area Of A Rectangle. What Goes In The Box ? The Area Of A Triangle. – PowerPoint PPT presentation
Number of Views:509
Avg rating:3.0/5.0
Title: Area Of Shapes.
1
Area Of Shapes.
2
What Is Area ?
Area is the amount of space inside a shape
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area
Area is measured in square centimetres.
A square centimetre is a square measuring one
centimetre in each direction.
It is written as
3
Estimating The Area.
Look at the four shapes below and use your
judgement to order them from smallest to largest
area
4
To decide the order of areas consider the four
shapes again
To measure the area we must determine how many
square centimetres are in each shape
Each shape is covered by 36 squares measuring a
centimetre by a centimetre .We can now see that
all the areas are equal at 36cm2 each.
5
Area Of A Rectangle.
Look again at one of the shapes whose area we
estimated
What was the length of the rectangle ?
9cm
How many rows of 9 squares can the breadth hold ?
4
We can now see that the area of the rectangle is
given by 9 x 4.
The formula for the area of a rectangle is
Area Length x Breadth
or
6
We can now calculate the area of each rectangle
very quickly
A L x B
A 12 x 3 36cm2
A L x B
A 6 x 6 36cm2
A L x B
A L x B
A 9 x 4 36cm2
A 18 x 2 36cm2
7
Example 1
Calculate the area of the rectangle below
Solution
This area is in square metres
A LB
Solution
A LB
L 7
B 4
L 3
B 5
A 7 x 4
A 3 x 5
A 28cm2
A 15m2
8
Example 3.
Solution.
Split the shape up into two rectangles
Calculate the area of A1 and A2.
2
3
5
6
Calculate the area of the shape above
Area A1 A2
Area ( 2 x 5) (6 x 3)
Area 10 18
Area 28cm2
9
What Goes In The Box ?
Find the area of the shapes below
48cm2
11.34m2
141cm2
10
The Area Of A Triangle.
Consider the right angled triangle below
What is the area of the triangle ?
Area ½ x 40 20cm2
What shape is the triangle half of ?
The formula for the area of a triangle is
Rectangle
Area ½ x Base x Height
What is the area of the rectangle?
A ½ BH
Area 8 x 5 40 cm2
11
Does the formula apply to all triangles ?
Can we make this triangle into a rectangle ?
Yes
The triangle is half the area of this rectangle
The areas marked A1 are equal.
The areas marked A2 are equal.
For all triangles Area ½ BH
12
Calculate the areas of the triangles below
Example 1
Example 2
Solution.
Solution.
Area ½ x base x height
Area ½ x base x height
height 6cm
base 10 cm
height 3.2m
base 6.4m
Area ½ x 10 x 6
Area ½ x 6.4 x 3.2
Area ½ x 60 30cm2
Area ½ x 20.48 10.24m2
13
Example 3.
Calculate the area of the shape below
Solution.
Divide the shape into parts
Area A1 A2
10
10
12
16-12 4
Area LB 1/2 BH
Area 10 x 12 ½ x 4 x 10
Area 120 20
Area 140m2
14
What Goes In The Box ? 2
Find the area of the shapes below
40cm2
32.13m2
258m2
15
The Area Of A Trapezium.
A Trapezium is any closed shape which has two
sides that are parallel and two sides that are
not parallel.
16
We are now going to find a formula for the area
of the trapezium
Area A1 ( A2 A3 )
Area b x h ½ x (a - b) x h
Area bh ½ h(a - b)
Divide the shape into parts
Area bh ½ ah ½ bh
Area ½ ah ½ bh
Work out the dimensions of the shapes
Area ½ h ( a b )
b
h
Often common sense is as good as the formula to
work out the area of a trapezium.
h
a b
17
Example 1
Calculate the area of the trapezium below
Solution ( Using the formula).
Area ½ h ( a b )
a 16
b 11
h 13
Area ½ x 13 x ( 16 11 )
Area ½ x 13 x 27
Area 175.5cm2
18
Solution ( Using composite shapes).
Divide the shape into parts
Area rectangle triangle
Area LB ½ BH
Area (11x 13) ( ½ x 5 x 13 )
Area 143 32.5
Area 175.5cm2
11
Decide for yourself if you prefer the formula or
composite shapes.
13
13
16 11 5
19
Example 2
Divide the shape into parts
Area rectangle triangle
Area LB ½ B H
A ( 10 x 8 ) ( ½ x 6 x 10 )
A 80 30
A 110 m 2
10
10
14 8 6
8
20
What Goes In The Box ? 3
Find the area of the shapes below
165cm2
19.85m2 (to 2 d.p)
21
The Area Of A Circle.
Consider the circle below divided into quarters
We are going to place the quarters as shown to
make the shape below
We can fit a rectangle around this shape
At the moment it is hard to see why this should
tell us how to calculate the area of a circle.
22
Now consider the same circle split into eight
parts
The eight parts are arranged into the same
pattern as last time
This time the shapes fit the rectangle more
closely
23
This time the shapes fit the rectangle more
closely
What length must the breadth B be close to ?
B r
What length must the length L be close to ?
Half of the circumference of the circle. If C
2 ? r then L ? r .
We now have an approximate length and breadth of
our rectangle.
24
? r .
What is the area of the rectangle ?
A ? r x r
A ? r 2
If the circle was split into more and more
smaller segments and the segments arranged in the
same pattern, then the parts would become the
rectangle shown above.
See Autograph Extras, New, Area Of Circle
for further info.
25
Find the area of the circles below
Example 2
Example 1.
A ? r 2
A ? r 2
r 1.35m
r 10
A 3.14 x 1.35 x 1.35
A 3.14 x 10 x 10
A 5.72m2 ( to 2 d.p)
A 314 cm2
26
Example 4
Example 3
Split the shape into two areas.
Find half the area of a circle
Area A1 A2
Area LB ½ ? r 2.
L 12
B 7
r 3.5
A 12 x 7 ½ x 3.14 x 3.5 x 3.5
A 84 19.23
A 76.93cm2
A 103.2cm 2. (to 1 d.p)
27
What Goes In The Box ? 4
Find the area of the shapes below
153.86cm2
31.16m2 ( 2 d.p)
35.1cm 2 ( 1 d.p)