Quadrilateral - PowerPoint PPT Presentation
1 / 25
Title:
Quadrilateral
Description:
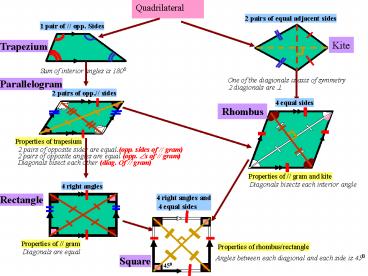
Quadrilateral 2 pairs of equal adjacent sides 1 pair of // opp. Sides Kite Trapezium Sum of interior angles is 1800 One of the diagionals is axis of symmetry – PowerPoint PPT presentation
Number of Views:150
Avg rating:3.0/5.0
Title: Quadrilateral
1
Quadrilateral
2 pairs of equal adjacent sides
1 pair of // opp. Sides
Kite
Trapezium
Sum of interior angles is 1800
One of the diagionals is axis of symmetry
Parallelogram
2 diagionals are ?
2 pairs of opp.// sides
4 equal sides
Rhombus
Properties of trapesium
2 pairs of opposite sides are equal.(opp. sides
of // gram)
2 pairs of opposite angles are equal (opp. ?s of
// gram)
Diagonals bisect each other (diag. Of // gram)
Properties of // gram and kite
Diagonals bisects each interior angle
4 right angles
Rectangle
4 right angles and 4 equal sides
Properties of // gram
Properties of rhombus/rectangle
Diagonals are equal
Angles between each diagional and each side is 450
Square
2
Trapeziums
Definition 1 pair of parallel sides
Properties
3
Parallelogram
Definition 2 pairs of opp. parallel sides
Properties
4
Conditions for Parallelogram
5
Rhombus
Definition a // gram or a kite of 4 equal sides
Properties
6
Rectangle
Definition a parallelogram of 4 right angles
Properties
7
Square
Definition a // gram of 4 right angles and 4
equal sides
Properties
2 pairs of opposite sides are equal.(opp. sides
of // gram)
8
Example 1 In the figure, PQRS is a kite
- Find x and y.
- Find the perimeter of the kite PQRS
PQ PS (given) x1 y3x-y2 (1) QRSR
(given)xy8 (2) (1)(2), 2x10 x5Put
x5 into (1), 5-y2 y3
(a)
(b)
PQ x1516? PQPSSRQR 6 6 8 8 28
9
Example 2 In the figure, ABCD is a kite. E is a
point of intersection of diagonals AC and BD,
AE9 cm, EC16 cm and DEEB12 cm
- Find the area of ABCD.
- Find the perimeter of ABCD
- ?ABC ?ADC (axis of symmetry AC)?AED900
Area of ?ADC
Area of kite ABCDArea of ?ABCArea of ?ADC
150150 300 cm2
In ?ADE, AD2AE2DE292122225 cm2 (Pyth
theorem) AD15 cm In ?CDE, DC2DE2EC2122162
400 cm2 (Pyth theorem) DC20 cm ? Perimeter
of ABCDADAB DCCB 15 15 20 20 70 cm
(b)
10
Example 3 In the figure, ABCD is a
parallelogram. Find x and y.
AD//BC (Given) x6801800 (prop. Of trapezium) ?
x1120(1500-y)2y1800 (prop. Of trapezium)
1500y1800 ? y1800 -1500300
11
Example 4 In the figure, ABCD is a
parallelogram. Find x and y.
?DAB?DCB (opp. ?s of // gram) x2003x-100 2x300
x150?DAB?CBA1800 (int.?s ,
AD//BC) x200y1800 150200y1800y1450
12
Example 5 In the figure, ABCD is a isosceles
trapezium with ABDC.Find x , y and z
AD//BC (Given) x12601800 (prop. Of trapezium) ?
x540
In ?ABE, AEDC (proof) ABAC (given)
?ABAE ? ya (base ?s. isos ? ) a x (corr.
?s. AE//DC) ? yx 540 yz1800 (prop.
Of trapesium)z 1800-540 1260
13
MID-POINT THEOREM
IF AM MB and AN NC then (a) MN // BC (b)
MN
(Abbreviation Mid-point theorem)
14
Example 13 In the figure, ABC is a triangle,
find x and y.
CEBE (given) ADDB (given)
(mid-point theorem)
DE//AC
x ?EDB 420
(corr. ?s , DE//AC)
(mid-point theorem)
15
Example 14 Prove that BPQR is a parallelgram
(given)
ARRB
(given)
AQQC
(mid-point theorem)
(given)
(opp-sides eq. And //)
16
Ex 11D
1(b)
BMMD (given) BNNC (given)
AMAC (given) BNNC (given)
(mid-point theorem)
(mid-point theorem)
17
Ex 11D
2(b)
APBP (given) AQCQ (given)
(mid-point theorem)
(corr.?s. PQ//BC)
In ?APQ, ?APQ ?PAQ a 1800 4601100a1800 a2
40
(adj ?s. on a st line)
18
3(a)
3(b)
B
C
D
9
19
4.
6
8
20
INTERCEPT THEOREM
B
P
A
D
C
Q
21
INTERCEPT THEOREM
22
INTERCEPT THEOREM
Proved
A
D
C
E
F
23
Example 15. AP//BQ//CR, ABBC, AP11 and CR5.
Find BQ.
A
B
C
11
5
P
Q
R
BQBSSQ 2.55.58
24
Example 16. AB and DC are straight lined. Find x
and y.
(a) Proved
A
E
D
Join DE through A and // BC
DE//PQ//BC
(given)
Q
P
(intercept theorem)
B
C
25
Example 16. Find QR and CD.
A
P
3
2
Q
B
6
R
C
8
S
D