Crystal defects/ Dislocations

1
Crystal defects/ Dislocations
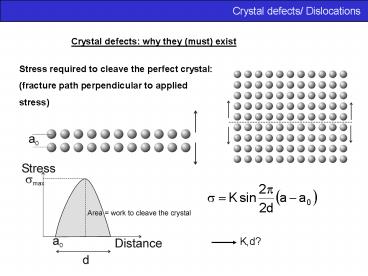
Crystal defects why they (must) exist
Stress required to cleave the perfect
crystal (fracture path perpendicular to
applied stress)
K,d?
2
Crystal defects/ Dislocations
1. What is K?
at a a0
3
Crystal defects/ Dislocations
2. What is d?
Equate area under curve (work to cleave crystal)
to surface energies of the two new surfaces
4
Crystal defects/ Dislocations
Element Direction E/GPa g/J/m2 smax/GPa smax/E
Gold lt111gt 110 1.35 27 0.25
Copper lt111gt 192 1.65 39 0.20
Diamond lt111gt 1,210 5.4 205 0.17
5
Crystal defects/ Dislocations
Stress required to shear the perfect crystal
Small displacements
Elastic behavior
Copper G 30.8 GPa, tmax 1.2 GPa
6
Crystal defects/ Dislocations
Copper E 129.8 GPa G 43.8 GPa
Theoretical shear strength 7.7 GPa
Theoretical cleavage strength 41.1 GPa
Actual tensile strength 0.1 GPa
Actual shear strength 0.05 GPa

• Main reasons for difference between theoretical
  and actual strength
• Stress concentrations at internal cracks
• Generation of dislocations

7
Crystal defects/ Dislocations
Line defects - DISLOCATIONS
Relevance metals, ceramics, glaciers, mountains,
earth-crust, millipeds, rugs,
History
Time Scientist Discovery
1900s Volterra, Timpe Dislocations in continuum elasticity
1934 1956 Orowan, Taylor, Polanyi Sir Peter Hirsch Device concept of dislocations in crystals Transmission electron microscopy of dislocations
8
Crystal defects/ Dislocations
Dislocation geometry
Two extreme cases edge and screw dislocations
Edge dislocation
No such crystal (simple cubic) in reality except
for Polonium below 36C. Edge dislocation would
normally split into partial dislocations.
9
Crystal defects/ Dislocations
Dislocation geometry
An edge dislocation can also be visualized as an
extra half plane (or missing half plane)
10
Crystal defects/ Dislocations
Dislocations general features
Dislocations are basic elements of plastic
deformation
As soon as critical shear stress is reached,
dislocation starts moving transition from
elastic to plastic deformation
Dislocation moves on glide plane.
After dislocation has left the crystal, crystal
is stress free. Many dislocations are necessary
to cause macroscopic deformation.
11
Crystal defects/ Dislocations
Dislocation geometry
Second elementary dislocation type screw
dislocations
Edge dislocation Burgers vector perpendicular to
dislocation line. Screw dislocation Burgers
vector parallel to dislocation line.
Looks like a parking ramp
12
Crystal defects/ Dislocations
Dislocations general features
Dislocations are basic elements of plastic
deformation
Slip produced by motion of two edge dislocations
13
Crystal defects/ Dislocations
Dislocations general features
Dislocations are basic elements of plastic
deformation
Slip produced by motion of many edge dislocations
14
Crystal defects/ Dislocations
Dislocations general features
Dislocations are basic elements of plastic
deformation
Slip produced by motion of screw dislocations
15
Crystal defects/ Dislocations
Dislocations general features
Closed dislocation loop
atoms shift parallel to
cut surface
16
Crystal defects/ Dislocations
Dislocations general features
Prismatic dislocation loop atoms shift
perpendicular to cut surface
17
Crystal defects/ Dislocations
Dislocations general features

• A dislocation is one-dimensional defect because
  the lattice is only disturbed along the
  dislocation line (apart from small elastic
  deformations which we do not count as defects
  farther away from the core). The dislocation line
  thus can be described at any point by a line
  vector t(x,y,z).
• In the dislocation core the bonds between atoms
  are not in an equilibrium configuration, i.e.
  at their minimum enthalpy value they are heavily
  distorted. The dislocation thus must possess
  energy (per unit of length) and entropy.
• Dislocations move under the influence of
  external forces which cause internal stress
  in a crystal. The area swept by the movement
  defines a plane, the glide plane, which
  always (by definition) contains the dislocation
  line vector.

18
Crystal defects/ Dislocations
Dislocations general features

• The movement of a dislocation moves the whole
  crystal on one side of the glide plane
  relative to the other side.
• (Edge) dislocations could (in principle) be
  generated by the agglomeration of point
  defects self-interstitial on the extra
  half-plane, or vacancies on the missing
  half-plane.

19
Crystal defects/ Dislocations
Dislocations general features Burgers vector

• Closed loop in perfect crystal
• Counterclockwise
• Burgers vector start to finish

Repeat same circuit for lattice with dislocation.
The vector pointing from the start to the finish
is the Burgers vector, b. Burgers vector of a
perfect dislocation is a lattice vector.
Closed circuit in perfect lattice from lattice
point to lattice point. Orientation of circuit
counterclockwise.
20
Crystal defects/ Dislocations
Dislocations general features
More on screw dislocations
Left hand screw dislocation
Right hand screw dislocation
21
Crystal defects/ Dislocations
Dislocations general features Burgers vector
Same for screw dislocation
Right-hand screw b opposite direction to
dislocation line
Left-hand screw b parallel to dislocation line
22
Crystal defects/ Dislocations
Dislocations general features Burgers vector
Bowman
23
Crystal defects/ Dislocations
Dislocation geometry
In general dislocations have mixed character
Make cut along AA, then shear the material along
the cut as shown with the arrows above. After
shearing, glue the atomic planes
together. Shear parallel to cut ? screw
dislocation shear perpendicular to cut ? edge
dislocation. (Note continuously changing
character along AA above)
24
Crystal defects/ Dislocations
Dislocations general features
Any forming process of metals (ice, glaciers,
mountains, metals) is governed by the density of
dislocations and their ability to move in the
material.
25
Crystal defects/ Dislocations
Dislocations different facets

1. Description of dislocations, general features
2. The stress field around dislocations (elastic
   properties)
3. Forces on and between dislocations
4. Moving dislocations
5. Dislocation multiplication
6. Dislocation reactions
7. Dislocations in fcc structures

26
Crystal defects/ Dislocations
Dislocations elastic properties
Why studying elastic properties of dislocations?
Compression

• Dislocations are sources for internal
  stresses.
• Elastic field surrounding dislocations interacts
  with other dislocations, with point defects,
  other defects, and with external stresses
  (similarity with electromagnetic fields).

Tension
Elastic properties and strain energies associated
with dislocations basis for strengthening
mechanisms, deformation mechanisms
27
Crystal defects/ Dislocations
Dislocations elastic properties
Curved dislocation
Mixed dislocation
28
Crystal defects/ Dislocations
Dislocations elastic properties displacements
for a screw dislocation
29
Crystal defects/ Dislocations
Dislocations elastic properties stress, strain
of screw dislocation
30
Crystal defects/ Dislocations
Dislocations elastic properties stress, strain
of edge dislocation
y
Hydrostatic compression above glide plane,
tension below ? Where do solute atoms go?
x
z
31
Crystal defects/ Dislocations
Dislocations elastic properties strain energy
Long-range stress field, at a distance of 104 b,
the stress is 10-4 G yield stress of soft
crystal
Singularity at center of dislocation
Distinguish between
dislocation core and
dislocation ? introduce cut-off at r0 b
Dislocation core continuum mechanics not valid,
energy obtained from atomistic simulations
32
Crystal defects/ Dislocations
Dislocations elastic properties strain energy
Calculation of strain energy
I. Determine local displacement, stress,
strain. Integrate over sample volume
II. Calculate work done in making displacement
across cut surface
33
Crystal defects/ Dislocations
Dislocations elastic properties self energy of
screw dislocation
Strain energy of a screw dislocation (per unit
length) Etotal Ecore Eelastic strain
G 10 GPa b 0.1 nm r0 1 nm R 1 mm ?
Eelastic 1 nJ/m
Eelastic aGb2
a 1
34
Crystal defects/ Dislocations
Dislocations elastic properties self energy of
screw dislocation
Strain energy of an edge dislocation (per unit
length) Etotal Ecore Eelastic strain
Eelastic aGb2/(1-n)
Self energy of edge dislocation slightly higher
than for screw dislocation
35
Crystal defects/ Dislocations
Dislocations elastic properties self energy
core vs. strain energy
Strain energy of a dislocation (per unit
length) Etotal Ecore Eelastic strain
Core energy 1/10 of bulk energy
36
Crystal defects/ Dislocations
Dislocations elastic properties self energy
Strain energy of a dislocation (per unit
length) Etotal Ecore Eelastic strain
How to choose R? Only one dislocation
in (single) crystal ? R sample size 10-1 m
Polycrystal R grain size or subgrain
size 10-4 m ? 60 variation in
self energy outside core
Al b 2.910-10 m, G 26.1 GPa, R 105 b ?
J/m ? J/atomic length
37
Crystal defects/ Dislocations
Dislocations elastic properties
Remember that the energy of a dislocation is
proportional to Gb2 !!
38
Crystal defects/ Dislocations
Dislocations different facets

1. Description of dislocations, general features
2. The stress field around dislocations (elastic
   properties)
3. Line tension, forces on and between dislocations
4. Moving dislocations
5. Dislocation reactions
6. Dislocation multiplication
7. Dislocation arrangements and grain boundaries
8. Strengthening mechanisms

39
Crystal defects/ Dislocations
Dislocations line tension
Strain energy of dislocation length of
dislocation ? Dislocation has line tension
(units energy per unit length) increase in
energy per unit increase in dislocation line
length
Downward force
Downward force per unit length dl
Additional force necessary to keep dislocation
line bowed.
40
Crystal defects/ Dislocations
Dislocations line tension
As a result of the line tension curved
dislocation lines experience a force and tend to
straighten out. Dislocation loops, for example,
would collapse due to the forces acting on curved
dislocations lines. Due to an inherent lattice
resistance to dislocation motion, the curved
dislocations can maintain their curvature.
41
Crystal defects/ Dislocations
Dislocations forces on dislocations

• Forces due to external stresses
• Forces due to internal stresses Same as for
  external stresses
• Forces due to other dislocations
• Chemical forces (climb, due to creation and
  annihilation of vacancies)

Unit tangent vector on dislocation line
Peach-Koehler equation
F tb
Often shear stress in direction of
b, force normal to dislocation line at any points
along the dislocation line
Use Peach-Koehler, simple geometries can be
treated by inspection.
42
Crystal defects/ Dislocations

1. Description of dislocations, general features
2. The stress field around dislocations (elastic
   properties)
3. Line tension, forces on and between dislocations
4. Moving dislocations
5. Dislocation multiplication
6. Dislocation reactions
7. Dislocation arrangements and grain boundaries
8. Strengthening mechanisms

43
Crystal defects/ Dislocations
Dislocations general features intersecting
dislocations
Jog (edge character)
Kinks (screw character)
44
Crystal defects/ Dislocations
Dislocations general features intersecting
dislocations

• Why are dislocation intersections important?
• With deformation dislocation density increases,
  intersections inevitable
• Intersections create jogs, kinks, can create
  vacancies. Jogs might slow down dislocation
  movement ? contribute to work hardening.
• Forest dislocations (dislocations intersecting
  glide planes of other dislocations) elastically
  interact with the glidedislocations and can
  impede the motion of thedislocations on the
  glide plane.

45
Crystal defects/ Dislocations
Dislocations general features intersecting
dislocations
Jog rule a jog is produced in a dislocation 1
if the Burgers vector of dislocation 2 is
normal to the dislocation line and the Burgers
vector of 1. The Burgers vector of the jog
(step height) is equal to the Burgers vector that
produced the jog.
46
Crystal defects/ Dislocations
Dislocations general features intersecting
dislocations
Two intersecting screw dislocations
Jog element with edge character ? Jog could only
move in PPRR plane. Movement of screw
dislocation in PQ direction pinned by jog PP
47
Crystal defects/ Dislocations
Dislocations general features intersecting
dislocations
48
Crystal defects/ Dislocations
Dislocations general features intersecting
dislocations
49
Crystal defects/ Dislocations
Dislocations general features intersecting
dislocations