Scalar Product

1
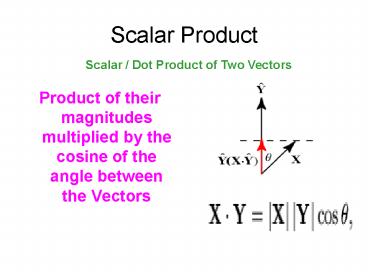
Scalar Product
Scalar / Dot Product of Two Vectors

• Product of their magnitudes multiplied by the
  cosine of the angle between the Vectors

2
Orthogonal Vectors

• Angular Dependence

3
Scalar Product

• Scalar Product of a Vector with itself ?
• A . A AA cos 0º
• A2

4
Scalar Product

• Scalar Product of a Vector and Unit vector ?
• x . A xAcosa
• Ax
• Yields the component of a vector in a direction
  of the unit vector
• Where alpha is an angle between A and unit vector
  x

5
Scalar Product

• Scalar Product of Rectangular Coordinate
• Unit vectors?
• x.y y.z z.x ?
• 0
• x.x y.y z.z ?
• 1

6
Scalar Product Problem 3

• A . B ?
• ( hint both vectors have components in three
  directions of unit vectors)

7
Scalar Product Problem 4

• A y3 z2 B x5 y8
• A . B ?

8
Scalar Product Problem 5

• A -x7 y12 z3
• B x4 y2 z16
• A.B ?

9
Line Integrals
10
Line Integrals
11
Line Integrals
12
Line Integrals
13
Line Integrals
14
Line Integrals
15
Line Integrals
16
Line Integrals
17
Spherical coordinates
18
Spherical coordinates
19
Spherical Coordinates

• For many mathematical problems, it is far easier
  to use spherical coordinates instead of Cartesian
  ones. In essence, a vector r (we drop the
  underlining here) with the Cartesian
  coordinates (x,y,z) is expressed in spherical
  coordinates by giving its distance from the
  origin (assumed to be identical for both
  systems) r, and the two angles  ? and 
  ? between the direction of r and the x-
  and z-axis of the Cartesian system. This sounds
  more complicated than it actually is  ? and  ?
   are nothing but the geographic longitude
•    and latitude. The picture below illustrates
  this

20
Spherical coordinate system
21
Simulation of SCS

• http//www.flashandmath.com/mathlets/multicalc/coo
  rds/index.html

22
Line Integrals
23
Line Integrals
24
Line Integrals
25
Line Integrals
26
Tutorial

• Evaluate

Where C is right half of the circle x2y216
Solution We first need a parameterization of the
circle.  This is given by, We now need a range
of ts that will give the right half of the
circle.  The following range of ts will do this

Now, we need the derivatives of the parametric
equations and lets compute ds
27
Tutorial

• The line integral is then

28
Assignment No 3

• Q. No. 1  Evaluate  where C is the curve
  shown below.

 
29
Assignment No 3 .

• Q.NO 2 Evaluate

were C is the line segment from   to