Lifting Bodies

1
Lifting Bodies

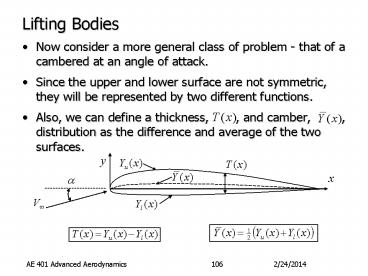
• Now consider a more general class of problem -
  that of a cambered at an angle of attack.
• Since the upper and lower surface are not
  symmetric, they will be represented by two
  different functions.
• Also, we can define a thickness, , and
  camber, , distribution as the difference
  and average of the two surfaces.

2
Lifting Bodies 2

• It will also be very useful to reverse these
  equations and define the upper and lower surfaces
  and functions of thickness and camber
• We also have to explicitly satisfy our surface
  tangency boundary condition on both surfaces, so
  by the above
• It seems the problem has doubled by having to
  deal with two surfaces.
• However, dealing with thickness and camber
  separately works well since we have already dealt
  with thickness.

3
Thin Airfoil Theory

• Now lets make Thin Airfoil assumptions consistent
  with this situation.
• If we once again assume the perturbation
  velocities are much less that the freestream then
  our BCs become
• Buried in these expressions is the further
  assumption that angle-of-attack is so small so
  that
• We can simplify these further by choosing to
  apply these at the y0 axis

4
Thin Airfoil Theory 2

• We know that we can use superposition to sum
  solutions
• So lets assume from the start that we will three
  solution contributions associate with freestream
  velocity, thickness and camber, respectively.
• The freestream component, for a flow at angle of
  attack, is already known
• Which has been simplified assuming small angles.
• To find the solutions for the other two terms,
  lets first make an assumption about how to
  satisfy the BCs.

5
Thin Airfoil Theory 3

• For the vertical flow velocity, we have three
  contributions
• So our boundary conditions can be written as
• Lets stipulate that our thickness potential will
  satisfy part of this BC - namely
• From our study of symmetric bodies, we know a
  solution for this is a source distribution whose
  strength is

6
Thin Airfoil Theory 4

• The source distribution satisfies the
  discontinuous jump in vertical velocity while
  having a continuous horizontal velocity given by
• These leaves the camber potential function to
  satisfy
• This equation says that the vertical velocity due
  to camber is continuous at y0, unlike that from
  thickness.
• However, we expect there to be a lifting surface
  to have a jump in pressure coefficient across the
  surface.

7
Thin Airfoil Theory 5

• But since, under Thin Airfoil Theory, the
  pressure coefficient is
• This implies that the horizontal velocity due to
  camber must be discontinuous
• We have one type of flow which satisfies this
  condition - vortex flow.
• If we assume the camber potential solution can be
  represented by a distributed vortex of strength
  ?(t)

8
Thin Airfoil Theory 6

• The horizontal velocities due to camber, on the
  y axis, are then
• We tackled this integral one before, when finding
  the vertical velocity due to a source
  distribution. Thus
• And just like the vertical velocity for a source,
  the horizontal velocity for a vortex jumps such
  that
• We can also try and find the vertical flow due to
  camber

9
Thin Airfoil Theory 7

• Which can only be reduced as far as a Cauchy
  Principal Value integral
• When this is combined with our remaining BC, we
  get
• Unfortunately, this equation cannot be reduced
  any further without knowing the camber line and
  using Appendix B.
• The really valuable result of all these
  assumptions is the ability to independently solve
  for thickness and camber effects.

10
Calculation of Forces

• In general, the forces normal and tangential to
  the horizontal (chord) line, can be found by
• However, if we us the thin airfoil
  approximations
• The two velocities due to thickness are equal and
  cancel.
• For a line vortex, the difference in camber
  velocities gives

11
Calculation of Forces 2

• Thus the normal force is simply
• Where G is the net strength of the vortex line.
• For the axial force, we need first find the upper
  and lower pressures independently using
  Bernoullis Eqn
• After throwing out all 2nd order and higher
  terms, this just becomes

12
Calculation of Forces 3

• After substituting the thin airfoil results for
  the perturbation velocities, the axial force
  integration becomes
• The first term vanishes for closed bodies. For
  open or blunt base bodies, there will be a little
  base drag.
• The second term, due to thickness, vanishes due
  to the symmetry of the integrand over the
  integration space.
• That leaves just the last term, that due to
  camber, to produce any axial force.

13
Calculation of Forces 4

• To evaluate what remains
• Replace the slope of the camber line with its
  boundary condition
• To get
• Once again, the second term vanishes due to
  symmetry of the integrand.

14
Calculation of Forces 5

• What remain is
• Thus, the forces on an airfoil look like
• When rotated into normal and tangential to the
  freestream velocity - I.e. lift and drag - we get

15
Calculation of Forces 6

• This result, that lift is proportional to the net
  circulation, is valid for all airfoils, not just
  thin ones.
• This effect has been given the name
  Kutta-Joukouski theorem, written in the vector
  form

• Look back to when we considered the cylinder
  (doublet) with a vortex at its center.
• We know can predict the lift force being
  generated without needing to know details about
  the pressures.

16
Calculation of Moment

• The last thing to discuss before setting out to
  solve our equations for a particular shape is the
  pitching moment.
• The moment taken about the leading edge will be
• By convention, a nose up moment is taken as
  positive.
• However, reviewing our solution for normal forces
  shows
• We will also want to locate the center of
  pressure - i.e. the point through which lift acts
  by