Plasma Heating

1
Plasma Heating

• Ohmic heating and its limit
• RF plasma heating
• Neutral beam heating

2
Ohmic Heating
Alcator scaling
3
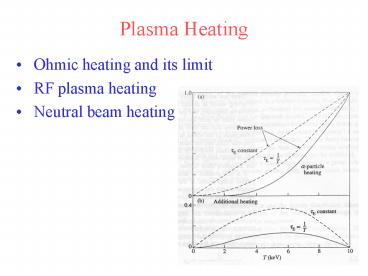
Ohmic Heating and its Limit

• Approximate plasma requirements for an ignited
  fusion reactor

• Ohmic heating cannot achieve high enough T
  unless J and B are very high

For 10keV,
4
Principle of Plasma Wave Heating
5
Collisionless Heating Mechanisms

• Landau damping
• Transit-time damping
• Wave resonances

6
Landau Damping
7
ECR Resonance Heating
8
General Considerations of RF Heating

• Basic idea Apply RF waves into plasmas, then
  propagate and be absorbed in plasma, thereby
  heating it.
• Waves applied to the edge of a plasma tend to be
  shielded out of the highly conducting plasma

• Externally applied RF waves can penetrate the
  plasma only by coupling to natural waves in the
  plasma determined by the plasma dielectric tensor
  

9
Plasma Dielectric Tensors

• Wave equations in plasma medium can be obtained
  from Maxwells equation by replacing j in terms
  of the electric field E. A dielectric tensor by
  equating the plasma current density j as a
  displacement current in a dielectric medium can
  complete the wave equation.

10
Plasma Dielectric Tensors

• Plasma current density can be obtained from the
  equation of motions of plasma particles, then
  cold plasma dielectric tensors

11
Dispersion Relation

• Dispersion relation for a plasma is generally
  obtained from the condition for nontrivial
  solutions for a homogeneous set of field
  equations, ie wave equations.

• Using a dielectric tensor of cold plasmas,

12
Dispersion Relations, Resonance, Cutoff
Astrom and Allis
For ? 0
Plasma oscillations
R waves
L waves
For ? ?/2
Extraordinary(X) waves
Ordinary(O) waves
Cutoff (n0)
Evanescent zone
Resonance (n??)
Cyclotron resonance
Hybrid resonance
13
Dispersion Relations, Resonance, Cutoff
For small electron mass,
For ? 0
For ? ?/2
where
14
Wave Normal Surfaces and CMA Diagram
Equation for wave normal surfaces with phase
velocity
15
Mode Conversion
Near resonance cold plasma model is no longer
valid since perpendicular phase velocity can no
longer be much larger than particle thermal
speeds. --gt kinetic approach

• Kinetic model distinguishes two channels of
  losing incident energy at resonance
• mode conversion to another propagating wave
• collisionless, wave-particle resonant interaction

16
Wave Properties near Resonance Region(upper
hybrid case)
17
Wave-Particle Collisionless Dissipation
Wave-particle resonance condition

• Landau resonance condition l0
• electron Landau damping for lower hybrid waves
  and for fast wave in the ICRF
• transit-time damping( or magnetic pumping) for
  fast wave in the ICRF
• Electron and ion cyclotron resonance condition
• normal and anomalous Doppler resonance

collision
Energetic particles
Maxwellian
High energy tail
18
Alfven Wave Heating
Low-frequency limit,
Shear Alfven wave
Compressional (fast magnetosonic)

• Launch compressional wave from outside and
  resonate on the shear-wave resonance surface

• TCA density increase, but no heating observed

19
Ion Cyclotron Range of Frequency Heating
For
Dispersion relations for

• Slow wave
• no propagation beyond ??i, need high-field
  launch
• mode conversion to electrostatic wave beyond edge

• Fast wave
• ion-ion hybrid resonance n//2S
• IBW mode conversion for high-field launch
• polarization match except fundamental mode
• --gt 2nd harmonic and minority heating

20
Second Harmonic Fast Wave and Bernstein Mode
Heating
21
Minority Ion Cyclotron Heating
Ion-ion hybrid resonance
Cyclotron resonance
Bernstein mode
22
Ion Bernstein Wave Heating
Slow wave
Fast wave
23
ICRF Heating Schematic
24
ICRF Heating Antenna
25
Lower Hybrid (LH) Heating
For LH frequency domain of
Dielectric tensor elements,
The uncoupled slow wave dispersion relation in
the LH domain
Cutoff at the so-called perpendicular Alfven
resonance
gives propagation requirement since Plt0,
26
LH Wave Accessibility Condition
Critical value for n//,
Launcher wavelength ?//,
Experimentally, slow waves are strongly damped
before reaching the resonance by electron Landau
damping since slow waves propagate at a small
angle to B
27
LH Heating/Current Drive
Grill for launching Lower Hybrid Wave
28
Electron Cyclotron Resonance Heating
Dispersion relations for cold plasmas
high-field launch
29
Electron Cyclotron Resonance

• For hot plasmas, both O- and X-modes have
  resonances at
• Strong absorbing resonances
• X-mode fundamental and second harmonic
• O-mode fundamental
• Accessibility conditions for these modes at

high-field low-field
O-mode
X-mode

• Accessible highest beta by X-mode ECH can be
  obtained from

30
Electron Cyclotron Resonance Heating
31
Wave Accessibility near ECR in Tokmak
32
Electron Cyclotron Resonance Region

• Resonance conditions with Doppler broadening

• Resonance conditions with relativistic effects

• for small relativistic effect

asymmetric

• Width of resonance