Double Pendulum Example

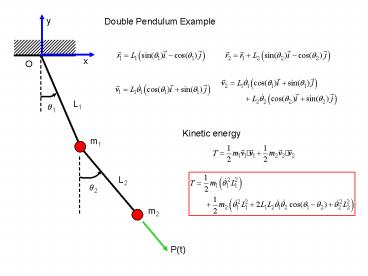
1
y
Double Pendulum Example
x
O
L1
q1
Kinetic energy
m1
L2
q2
m2
P(t)
2
Potential energy
k1
Virtual work
L1
q1
k2
m1
L2
torsional springs
q2
m2
so
P
3
Algebra Lots, and lots of algebra
4
From virtual work
Equations of motion
5
Write in Matrix form
where
or
First-order form
State vector
6
Matlab
Create an m-fiile that returns derivative vector
function describes the EOM for a double
pendulum. In 2nd-order form, EOM's take the
form Mq_ddot F
function xprime ...double_pend(t,x,g,L1,L2,m1,m
2,k1,k2,P,c1,c2) th1 x(1) th2 x(2) th1d
x(3) th2d x(4) M (m1m2)L12
(m2L1L2cos(th1-th2)) (m2L1L2cos(th1-th
2)) m2L22 centripetal terms Q1c
-m2L1L2sin(th1-th2)th2d2 Q2c
m2L1L2sin(th1-th2)th1d2 gravity
terms Q1g - (m1m2)gL1sin(th1) Q2g -
m2gL2sin(th2)
continued
7
follower-force terms Q1F PL1sin(th2-th1) Q2
F 0 spring terms Q1k - (k1k2)th1
k2th2 Q2k k2th1 - k2th2 damper
terms Q1d - (c1c2)th1d c2th2d Q2d
c2th1d - c2th2d F (Q1cQ1gQ1FQ1kQ1d)
(Q2cQ2gQ2FQ2kQ2d) xprime x(3) x(4)
M\F
The backslash command efficiently solves MxF
8
Matlab calling script
ME6441, Dr. Ferri generates response to
double-pendulum. Script calls the function
double_pend.m g9.81 L1 1 L2 1.7 m11
m22 k1 10 k2 10 P -100 c1.2
c2.2 t0 0 tf 20 options
odeset('reltol',1e-7,'abstol',1e-7) f_anon
_at_(t,q) double_pend(t,q,g,L1,L2,m1,m2,k1,k2,P,c1,c2
) t,x ode45(f_anon,t0 tf,0 1 0
0',options) th1 x(,1) th2 x(,2) th1d
x(,3) th2d x(,4) figure(1) plot(t,th1,t
,th2,'--','linewidth',2) xlabel('time
(sec)') ylabel('\theta_1 and \theta_2
(rad)') legend('\theta_1','\theta_2')
9
(No Transcript)