Measuring g with a Pendulum

1
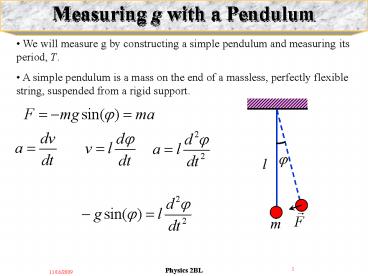
Measuring g with a Pendulum

• We will measure g by constructing a simple
  pendulum and measuring its period, T.
• A simple pendulum is a mass on the end of a
  massless, perfectly flexible string, suspended
  from a rigid support.

2
Measuring g with a Pendulum
Can we solve this differential equation?
Looks rather tough to me. Needs a simplification.
when is small
Harmonic oscillation with frequency w, and
period
3
Measuring g with a Pendulum
What assumptions have been made? m is a point
mass, so that l is measured from the point of
suspension to the point mass. (The center of mass
will be a good approximation to a point mass.)
The mass of the string is negligible relative
to m. (We can ensure this by choosing the correct
material for the string and sufficient mass for
m). Rigid support.
4
Measuring g with a Pendulum
If we want to measure g using the simple
pendulum, we will need to keep the amplitude of
the swing small enough so that How closely must
the equivalence hold for our purposes? Therefore,
how small must the angle be? How can you test
empirically if the angle is small enough? Our
equation of motion also does not include any air
friction so that we must make certain that it is
a small force relative to the gravity force that
makes the pendulum oscillate. How can you test
for the influence of friction?
5
Two types of measurement errors

• Random Errors
• Can be reduced by repeated measurements.
• Can also be estimated by repeated measurement.
• Example measure the fraction of people over 6
  by surveying 100 people from around the world.
• Systematic Errors
• Harder to estimate and reduce.
• Calibration errors, neglecting small corrections,
  or mistakes.
• Example measure the fraction of people over 6
  by surveying a group from France.

6
Error Propagation
What is the perimeter of this figure?
p w x y z
You measure w, x, y, z, and compute p.
How would you calculate the error on p?

• First, you estimate errors from w, x, y, z. They
  all are likely to be on the order of precision of
  the ruler, 1/32 or 0.7 mm.
• Next, you propagate them following certain rules
  to compute the error on p.

7
Error Propagation
p w x y z
We estimate errors on w, x, y, and z, as
What is our estimate of error on p?
Since ,
However, since dx, dy, dz and dw are all error
estimates, we do not know the signs of the actual
errors. Therefore, it could be
OR
We would normally use the rule of addition in
quadrature
8
The formula for error analysis.
What if we want to subtract the two lengths?
Our best estimate of the difference is 1 mm
-
We estimate the error by addition as quadrature
as before
The error of the difference is the same as the
error of the sum
While the result for the sum is reasonable, the
result for the difference seems to be rather bad
we cant even say, if it is positive or
negative.
9
The formula for error analysis.
While the result for the sum is reasonable, the
result for the difference seems to be rather bad
we cant even say positive or negative
Fractional error
Subtracting two close numbers is a bad idea!
Fractional errors soar!
What else are fractional errors good for?
10
The formula for error analysis.
What else are fractional errors good for?
How do we calculate the error of knowing the
error of ?
Lets try to plug in some numbers
The error of becomes large as goes to
zero. Thats we the observer on the beach was
recommended to stay at some reasonable altitude.
11
The formula for error analysis.
From and
we calculate ,
then
Now we have got with

Next we need to calculate the error of
The rule for products and quotients is to add
the relative errors in quadrature
Lets assume
12
The formula for error analysis.
Now we have got
where
And we have just calculated Where do we
go from here?
Does the coefficient contribute to the
error?
It depends, what kind of error. It certainly
contributes to the absolute error, but it does
NOT contribute to the FRACTIONAL arror.
Are we there yet?! almost
13
The formula for error analysis.
We have never discussed, how we compute the error
of - the 1st step the in calculation.
is the length of the string, is the angle
with the horizontal
the general formula
has to be measured in radians, NOT degrees.
14
The formula for error analysis.
the general formula
Suppose, we can measure the angle, q, with a
precision of 1 or 0.02 rad.
If the string is near horizontal, q 10, the
contribution to the error is
- large fractional error
If the string is near vertical, q 80, the
contribution to the error is
- tiny fractional error
15
The formula for error analysis.
Error propagation step by step is a long a
tedious procedure Are there any shortcuts?!
Actually, there are. For any function
of independent variables
I am not sure, you see THIS as a shortcut, but it
is a kind of.
16
Step by step or partial derivative? Which way of
suffering is nobler?
Going step by step would be pretty easy, BUT we
can NOT do it!
Example
Because at least variable, x, appears in the
equation more than once! And the two xs are NOT
independent variables, because they are the SAME
variable.
In a case like that, you absolutely have to use
the partial derivative way!