Some Remarks on Subdivision Curves

1
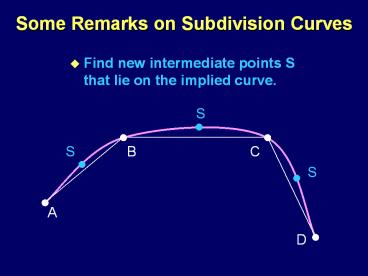
Some Remarks on Subdivision Curves

• Find new intermediate points S that lie on the
  implied curve.

S
B
C
S
S
A
D
2
Quadratic Interpolating Subdivision

• Cannot generally fit a parabola thru 4 points

B
C
A
D
3
Quadratic Interpolating Subdivision

• Cannot generally fit a parabola thru 4 points
• ? Interpolate between two separate parabolas

S
B
C
A
D
4
Cubic Interpolating Subdivision

• 4-point cubic interpolation in the plane
  S 9B/16 9C/16 A/16 D/16 S
  M (B A)/16 (C D)/16

S
B
C
M
A
D
5
Application of Subdivision Step
Original data points and control polygon
Focus on 4 consecutive points A, B, C, D Create
a corresponding subdivision point S
S
6
Yet Another Conceptual Approach
Original data points and control polygon
Focus on 4 consecutive points A, B, C, D ?
Blend between two circular arcs !
7
Circle Spline Construction (1)
Original data points and control polygon
Focus on 4 consecutive points A, B, C, D
LEFT CIRCLE thru A, B, C
8
Circle Spline Construction (2)
Original data points and control polygon
Focus on 4 consecutive points A, B, C, D
LEFT CIRCLE thru A, B, C
RIGHT CIRCLE thru B, C, D
9
Circle Spline Construction (3)

• left circle bisector ? SLright circle
  bisector ? SR
• average btw. SL and SR ? S

SL
S
SR
10
Circle Spline Construction (4)
RECURSE !
S
Cannot guarantee convergence behavior !
11
A Better Circle Spline
Not based on subdivision, but on iterated
interpolation.
How should this blending be done ? ...
12
Blending With Intermediate Circles (1)

• Left Circle thru A, B, C Right Circle thru B,
  C, D.

Draw Tangent Vectors for both circles at B and C.
D
B
C
A
13
Blending With Intermediate Circles (2)

• Left Circle thru A, B, C Right Circle thru B,
  C, D.

Draw Tangent Vectors for both circles at B and C.
Draw a bundle of regularly spaced Tangent Vectors.
D
B
C
A
14
Blending With Intermediate Circles (3)

• Left Circle thru A, B, C Right Circle thru B,
  C, D.

Draw Tangent Vectors for both circles at B and C.
Draw a bundle of regularly spaced Tangent Vectors.
Draw n equal-angle-spaced Circles from B to C.
D
B
C
A
15
Blending With Intermediate Circles (4)

• Left Circle thru A, B, C Right Circle thru B,
  C, D.

Draw Tangent Vectors for both circles at B and C.
Draw a bundle of regularly spaced Tangent Vectors.
Draw n equal-angle-spaced Circles from B to C.
D
Make n equal segments on each arc andchoose uth
point on uth circle.
B
C
A
? G1-continuity _at_ B, C
16
REFERENCE TO LEARN MORE

• C. H. Séquin, K. Lee, and J. Yen
• Fair G2 and C2-Continuous Circle Splinesfor
  the Interpolation of Sparse Data Points
• JCAD Vol 37, No 2, pp 201-211, Feb. 2005.