PHYSICS 231 Lecture 34: Oscillations - PowerPoint PPT Presentation
1 / 18
Title:
PHYSICS 231 Lecture 34: Oscillations
Description:
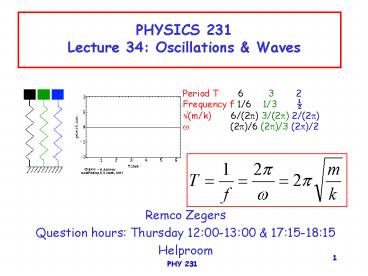
Helproom. Period T 6 3 2. Frequency f 1/6 1/3 (m/k) 6/(2 ) 3 ... elevator. moon. m. L. PHY 231. 7. example: the height of the lecture room. demo. PHY 231. 8 ... – PowerPoint PPT presentation
Number of Views:74
Avg rating:3.0/5.0
Title: PHYSICS 231 Lecture 34: Oscillations
1
PHYSICS 231Lecture 34 Oscillations Waves
Period T 6 3 2 Frequency f
1/6 1/3 ½ ?(m/k) 6/(2?) 3/(2?)
2/(2?) ? (2?)/6 (2?)/3 (2?)/2
- Remco Zegers
- Question hours Thursday 1200-1300
1715-1815 - Helproom
2
Harmonic oscillations vs circular motion
v0
t0
t1
t2
v0?r?A
??t
??t
t3
t4
v0
?
vx
?
A
3
A
xharmonic(t)Acos(?t)
x
time (s)
-A
?2?f2?/T?(k/m)
A?(k/m)
vharmonic(t)-?Asin(?t)
-A?(k/m)
aharmonic(t)-?2Acos(?t)
a
4
Another simple harmonic oscillation the pendulum
Restoring force F-mgsin? The force pushes the
mass m back to the central position. sin??? if
? is small (lt150) radians!!! F-mg? also
?s/L so F-(mg/L)s
5
pendulum vs spring
parameter spring pendulum
restoring force F F-kx F-(mg/L)s
period T T2??(m/k) T2??(L/g)
frequency f f?(k/m)/(2?) f?(g/L)/(2?)
angular frequency ??(k/m) ??(g/L)
6
example a pendulum clock
- The machinery in a pendulum clock is kept
- in motion by the swinging pendulum.
- Does the clock run faster, at the same speed,
- or slower if
- The mass is hung higher
- The mass is replaced by a heavier mass
- The clock is brought to the moon
- The clock is put in an upward accelerating
- elevator?
L? m? moon elevator
faster
same
slower
7
example the height of the lecture room
demo
8
damped oscillations
In real life, almost all oscillations eventually
stop due to frictional forces. The oscillation
is damped. We can also damp the oscillation on
purpose.
9
Types of damping
No damping sine curve
Under damping sine curve with decreasing amplitude
Critical damping Only one oscillations
Over damping Never goes through zero
10
Waves
The wave carries the disturbance, but not the
water
position y
position x
Each point makes a simple harmonic vertical
oscillation
11
Types of waves
wave
oscillation
Transversal movement is perpendicular to the
wave motion
oscillation
Longitudinal movement is in the direction of the
wave motion
12
A single pulse
velocity v
time to
time t1
x0
x1
v(x1-x0)/(t1-t0)
13
describing a traveling wave
? wavelength distance between two maxima.
While the wave has traveled one wavelength,
each point on the rope has made one period of
oscillation.
v?x/?t?/T ?f
14
example
2m
- A traveling wave is seen
- to have a horizontal distance
- of 2m between a maximum
- and the nearest minimum and
- vertical height of 2m. If it
- moves with 1m/s, what is its
- amplitude
- period
- frequency
2m
- amplitude difference between maximum (or
minimum) - and the equilibrium position in the vertical
direction - (transversal!) A2m/21m
- v1m/s, ?22m4m T?/v4/14s
- f1/T0.25 Hz
15
sea waves
An anchored fishing boat is going up and down
with the waves. It reaches a maximum height every
5 seconds and a person on the boat sees that
while reaching a maximum, the previous waves has
moves about 40 m away from the boat. What is the
speed of the traveling waves?
Period 5 seconds (time between reaching two
maxima) Wavelength 40 m v ?/T40/58 m/s
16
Speed of waves on a string
F tension in the string ? mass of the string per
unit length (meter)
screw
tension T
example violin
L
M
v ?/T ?f?(F/?) so f(1/?)?(F/?) for fixed
wavelength the frequency will go up (higher tone)
if the tension is increased.
17
example
- A wave is traveling through the
- wire with v24 m/s when the
- suspended mass M is 3.0 kg.
- What is the mass per unit length?
- What is v if M2.0 kg?
a) Tension Fmg39.829.4 N v?(F/?) so
?F/v20.05 kg/m b) v?(F/?)?(29.8/0.05)19.8
m/s
18
bonus -)
The block P carries out a simple harmonic motion
with f1.5Hz Block B rests on it and the surface
has a coefficient of static friction ?s0.60. For
what amplitude of the motion does block B slip?
The block starts to slip if FfrictionltFmovement ?s
n-maP0 ?smgmaP so ?sgaP ap -?2Acos(?t)
so maximally ?2A2?fA ?sg2?fA A
?sg/2?f0.62 m