Efficiently Solving Convex Relaxations for

1
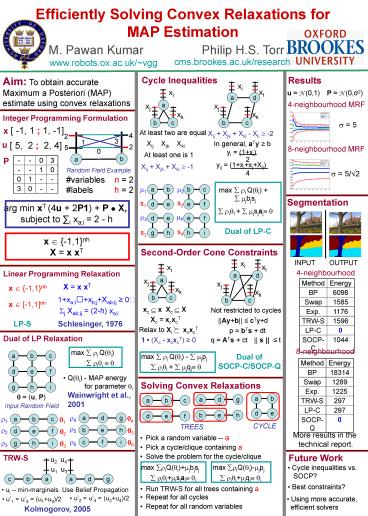
Efficiently Solving Convex Relaxations for MAP
Estimation
Aim To obtain accurate Maximum a Posteriori
(MAP) estimate using convex relaxations
Cycle Inequalities
Results
xi
xl
xi
u N (0,1)
P N (0,s2)
a
d
4-neighbourhood MRF
a
xj
xj
xk
xk
Integer Programming Formulation
b
c
b
c
? 5
-1, 1 1, -1
x
At least two are equal
Xij Xjk Xkl - Xli ? -2
4
2
3
1
Xij Xjk Xki
u
In general, aTy b
5, 2 2, 4
2
5
8-neighbourhood MRF
0
yi (1xi)
At least one is 1
b
a
2
P
yij (1xixjXij)
Xij Xjk Xki ? -1
Random Field Example
4
? 5/v2
variables n 2 labels h 2
a
b
b
c
?1
?2
max ? ?i Q(?i) ? ?jbjsj
Segmentation
s2
s1
d
e
e
f
arg min xT (4u 2P1) P ? X, subject to ?i
xai 2 - h x ? -1,1nh X x xT
? ?i?I ? ?jsjaj? ?
?4
?3
d
e
e
f
Dual of LP-C
s4
s3
g
h
h
i
Second-Order Cone Constraints
INPUT
OUTPUT
xi
xl
xi
4-neighbourhood
Linear Programming Relaxation
a
d
a
xj
xj
X x xT
x ? -1,1nh
xk
xk
b
c
1xaixbjXabij 0
b
c
x ? -1,1nh
xc ? x Xc ? X
?j Xabij (2-h) xai
Not restricted to cycles
Xc xcxcT
Ayb cTyd
LP-S
Schlesinger, 1976
p bTs dt
Dual of LP Relaxation
1 (Xc - xcxcT) 0
q ATs ct
s t
8-neighbourhood
max ? ?i Q(?i)
a
b
c
Dual of SOCP-C/SOCP-Q
max ? ?i Q(?i) - ? ?jpj
? ?i?i ? ?
? ?i?I ? ?jqj? ?
d
e
f

• Q(?i) - MAP energy
• for parameter ?i

Solving Convex Relaxations
g
h
i
Wainwright et al., 2001
? (u, P)
a
b
a
d
g
a
b
c
Input Random Field
d
e
b
e
h
d
e
f
a
d
g
?4
?4
a
b
c
?1
?1
CYCLE
TREES
?5
b
e
h
?2
?5
d
e
f
?2
More results in the technical report.

• Pick a random variable -- a

c
f
i
?6
?6
g
h
i
?3
?3

• Pick a cycle/clique containing a

• Solve the problem for the cycle/clique

Future Work
TRW-S
u2
u4
max ??iQ(?i)?jbjsj
max ??iQ(?i)-?jpj

• Cycle inequalities vs.
• SOCP?

u1
u3
? ?i?I?jsjaj? ?j
? ?i?I?jqj? ?j
c
b
a
a
d
g

• Best constraints?

• Run TRW-S for all trees containing a

• ui -- min-marginals. Use Belief Propagation

• Repeat for all cycles

• u2 u4 (u2u4)/2

• Using more accurate,
• efficient solvers

• u1 u3 (u1u3)/2

• Repeat for all random variables

Kolmogorov, 2005