Ch. 15: Data Clustering

1
Ch. 15 Data Clustering
Ch.15.1 Motivation

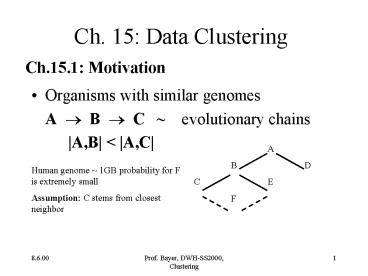
• Organisms with similar genomes
• A ? B ? C evolutionary chains
• A,B lt A,C

A B D C E F
Human genome 1GB probability for F is extremely
small Assumption C stems from closest neighbor
2
More Examples

• Stocks with similar behavior in market
• Buying basket discovery
• Documents on similar topics
• ? nearest neighbors?
• ? similarity or distance measures?

3
Supervised vs. Unsupervised Classification
Supervised set of classes (clusters) is given,
assign new pattern (point) to proper cluster,
label it with label of its cluster Examples
classify bacteria to select proper antibiotics,
assign signature to book and place in proper
shelf Unsupervised for given set of patterns,
discover a set of clusters (training set) and
assign addtional patterns to proper
cluster Examples buying behavior, stock groups,
closed groups of researchers citing each other,
more?
4
Components of a Clustering Task

• Pattern representation (feature extraction), e.g.
  key words, image features, genes in DNS sequences
• Pattern proximity similarity, distance
• Clustering (grouping) algorithm
• Data abstraction representation of a cluster,
  label for class, prototype, properties of a class
• Assessment of quality of output

5
Examples

• Clustering of documents or research groups by
  citation index, evolution of papers. Problem
  find minimal set of papers describing essential
  ideas
• Clustering of items from excavations according to
  cultural epoques
• Clustering of tooth fragments in anthropology
• Carl von Linne Systema Naturae, 1735, botanics,
  later zoology
• etc ...

6
Ch. 15.2 Formal Definitions
Pattern (feature vector, measurements,
observations, data points) X ( x1, ... , xd) d
dimensions, measurements, often d not fixed, e.g.
for key words Attribute, Feature xi
Dimensionality d Pattern Set H X1, X2,
... , Xn H often represented as n?d pattern
matrix Class set of similar patterns, pattern
generating process in nature, e.g. growth of
plants
7
More Definitions
Hard Clustering classes are disjoint, every
pattern gets a unique label from L l1, l2,
... , ln with li ? 1, ... , k see Fig.
1 Fuzzy Clustering pattern Xi gets a
fractional degree of membership fij for each
output cluster j Distance Measure metric or
proximity function or similarity function in
feature space to quantify similarity of patterns
8
Ch. 15.3 Pattern Representation and Feature
Selection
Human creativity Select few, but most
relevant features !!! Cartesian or polar
Coordinates? See Fig. 3 Document retrieval key
words (which) or citations? What is a good
similarity function? Use of thesaurus? Zoology
Skeleton, lungs instead of body shape or living
habits dolphins, penguins, ostrich!!
9
Types of Features

• Quantitative continuous, discrete, intervals,
  fuzzy
• Qualitative enumeration types (colors), ordinals
  (military ranks), general features like
  (hot,cold), (quiet, loud) (humid, dry)
• Structure Features oo hierarchies like vehicle
  ? car ? Benz ? S400 vehicle ? boat ? submarine

10
Ch. 15.4 Similarity Measures
Similar small distance Similarity function
not necessarily a metric, triangle inequality
dist (A,B) dist (B,C) ? dist (A,C)
may be missing, quasi metric. Euclidean
Distance dist2 (Xi,Xj) (?k1d xi,k - xj,k
²)1/2 Xi - Xj 2 Special case of Minkowski
metric distp (Xi,Xj) (?k1d xi,k - xj,k
p)1/p Xi - Xj p
11
Proximity Matrix for n patterns with symmetric
similarity n (n-1)/2 similarity
values Representation problem mixture of
continuous and discontinuous attributes,
e.g. dist ((white, -17), (green, 25)) use
wavelength as value for colors and then Euclidean
distance???
12
Other Similarity Functions
Context Similarity s(Xi , Xk ) f(Xi , Xk,
E) for environment E e.g. 2 cars on a country
road 2 climbers on 2 different towers of 3
Zinnen mountain neighborhood distance of Xk w.r.
to Xi nearest neighbor number NN(Xi ,
Xk ) mutual neighborhood distance MND(Xi , Xk )
NN(Xi , Xk ) NN(Xk , Xi )
13
Lemma MND(Xi , Xk ) MND(Xk , Xi ) MND(Xi ,
Xi ) 0 Note MND is not a metric, triangle
inequality is missing! see Fig. 4 NN(A,B)
NN(B,A) 1 MND(A,B) 2 NN(B,C) 2 NN(C,B)
1 MND(B,C) 3 see Fig. 5 NN(A,B) 4 NN(B,A)
1 MND(A,B) 5 NN(B,C) 2 NN(C,B)
1 MND(B,C) 3
14
(Semantic) Concept Similarity
s (Xi , Xk ) f (Xi , Xk , C, E) for
concept C, environment E Examples for C ellipse,
rectangle, house, car, tree ... See Fig. 6
15
Structural Similarity of Patterns
(5 cyl, Diesel, 4000 ccm) (6 cyl, gasoline,
2800 ccm) dist ( ... ) ??? dist (car, boat)
??? ? how to cluster car engines? Dynamic, user
defined clusters via query boxes?
16
Ch. 15.5 Clustering Methods

• agglomerative merge clusters versus
  divisive split clusters
• monothetic all features at once versus
  polythetic one feature at a time
• hard clusters pattern in single class versus
  fuzzy clusters pattern in several classes
• incremental add pattern at a time versus non-incre
  m. add patterns at once (important for large
  data sets!!)

17
Ch. 15.5.1 Hierarchical Clusteringby
Agglomeration
Single Link
C2
C1
dist (C1, C2) min dist (X1, X2 ) X1?C1,
X2?C2
18
Complete Link
C2
C1
dist (C1, C2) max dist (X1, X2 ) X1?C1,
X2?C2 Merge clusters with smallest distance in
both cases! Examples Figures 9 to 13
19
Hierarchical algglomerative clustering
algorithmfor single link and complete link
clustering
1. Compute proximity matrix between pairs of
patterns, initialize each pattern as a cluster 2.
Find closest pair of clusters, i.e. sort n2
distances with O(n2log n), merge clusters,
update proximity matrix (how, complexity?) 3. if
all patterns are in one cluster then stop
else goto step 2 Note proximity matrix
requires O(n2) space and for distance computation
at least O(n2) time for n patterns (even without
clustering process), not feasible for large
datasets!
20
Ch. 15.5.2 Partitioning Algorithms
Remember agglomerative algorithms compute a
sequence of partitions from finest (1 pattern per
cluster) to coarsest (all patterns in a single
cluster). The number of desired clusters is
chosen at the end by cutting the dendogram at a
certain level. Partitioning algorithms fix the
number k of desired clusters first, choose k
starting points (e.g. randomly or by sampling)
and assign the patterns to the closest cluster.
21
Def. A k-partition has k (disjoint)
clusters. There are nk different k-partitions for
a set of n patterns. What is a good
k-partition? Squared Error Criterion Assume
pattern set H is divided into k clusters labeled
by L and li ? 1, ... ,k Let cj be the
centroid of cluster j, then the squared error
is e2 (H,L) ?j1k?i1 nj Xij - cj 2 Xij
jth pattern of cluster j
22

• Sqared Error Clustering Algorithm (k-means)
• 1. Choose k cluster centers somehow
• 2. Assign each pattern to ist closest cluster
  center O(nk)
• 3. Recompute new cluster centers cj and e2
• 4. If convergence criterion not satisfied
  then goto step 2 else exit
• Convergence Criteria
• few reassignments
• little decrease of e2

23

• Problems
• convergence, speed of convergence?
• local minimum of e2 instead of global minimum?
  This is just a hill climbing algorithm.
• therefore several tries with different sets of
  starting centroids
• Complexities
• time O(nkl) l is number of iterations
• space O (n) disk and O(k) main storage space

24
Note simple k-means algorithm is very sensitive
to initial choice of clusters -gt several runs
with different initial choices -gt split and
merge clusters, e.g. merge 2 clusters with
closest centers and split cluster with
largest e2 Modified algorithm is ISODATA
algorithm
25
ISODATA Algorithm 1. choose k cluster centers
somehow, heuristics 2. assign each pattern to its
closest cluster center O(nk) 3. recompute new
cluster centers cj and e2 4. if convergence
criterion not satisfied then goto step 2 else
exit 5. merge and split clusters according to
some heuristics Yields more stable results than
k-means in practical cases!
26
Minimal Spanning Tree clustering 1. Compute
minimal spanning tree in O (mlog m) where m is
the number of edges in graph, i.e. m n2 2.
Break tree into k clusters by removing the k-1
most expensive edges from tree Ex see Fig. 15
27
Representation of Clusters hard clusters
equivalence classes 1. Take one point as
representative 2. Set of members 3. Centroid
(Fig. 17) 4. Some boundary points 5. Bounding
polygon 6. Convex hull (fuzzy) 7. Decision tree
or predicate (Fig. 18)
28
Genetic Algorithms with k-means
Clustering Pattern set H X1, X2, ... ,
Xn labeling L l1, l2, ... , ln with
li ? 1, ... , k generate one or several
labelings Li to start solution genome or
chromosome B b1 ? b2 ? ... ? bn B is
binary encoding of L with bi fixed length
binary representation of li Note there are 2 n
ld k points in the search space for solutions,
gigantic! Interesting cases n gtgt 100. Removal of
symmetries and redundancies does not help much.
29
Fitness function inverse of squared error
function. What is the optimum? Genetic
operations crossover of two chromosomes b1
? b2 ? ... bi ? ... ? bn c1 ? c2 ? ...
ci ? ... ? cn results in two new solutions,
decide by fitness function b1 ? b2 ? ... ci ?
... ? cn c1 ? c2 ? ... bi ? ... ? bn
30
Genetic operations continued mutation invert 1
bit, this guarantees completeness of search
procedure. Distance of 2 solutions number of
different bits selection probabilistic choice
from a set of solutions, e.g. seeds that grow
into plants and replicate (natural selection).
Probabilistic choice of centroids for
clustering. exchange of genes replication of
genes at another place Integrity constraints for
survival (mongolism) and fitness functions for
quality. Not all genetic modifications of nature
are used in genetic algorithms!
31
Example for Crossover S1 01000 S2 11111 S1
01000 S2 11111 crossover yields S3
01111 S4 11000 for global search see Fig. 21
32
K-clustering and Voronoi Diagrams C1 C2
C3 C6 C4 C5
33
Difficulties

• how to choose k?
• how to choose starting centroids?
• after clustering, recomputation of centroids
• centroids move and Voronoi partitioning changes,
  e.i. reassignment of patterns to clusters
• etc.

34

• Example 1 Relay stations for mobile phones
• Optimal placement of relay stations optimal
  k-clustering!
• Complications
• points correspond to phones
• positions are not fixed
• number of patterns is not fixed
• how to choose k ?
• distance function complicated 3D geographic
  model with mountains and buildings, shadowing,
  ...

35

• Example 2 Placement of Warehouses for Goods
• points correspond to customer locations
• centroids correspond to locations of warehouses
• distance function is delivery time from
  warehouse multiplied by number of trips, i.e.
  related to volume of delivered goods
• multilevel clustering, e.g. for post office,
  train companies, airlines (which airports to
  choose as hubs), etc.

36
Ch. 15.6 Clustering of Large Datasets
Experiments reported in Literature clustering of
60 patterns into 5 clusters and comparison of
various algorithms using the encoding of genetic
algorithms length of one chromosome 60
ceiling(ld(5)) 180 bits each chromosome 1
solution, i.e. 260ceiling(ld(5)) 2180
100018 1054 points in the search space for
optimal solution Isolated experiments with 200
points to cluster
37
Examples clustering pixels of 500?500 image
250.000 points documents in Elektra gt 1 Mio
documents see Table 1 ? above problems
prohibitive for most algorithms, only candidate
so far is k-means
38
Properties of k-means Algorithm

• Time O (nkl)
• Space O (k n ) to represent H, L, dist (Xi,
  centroid(li ))
• solution is independent of order in which
  centroids are chosen, order in which points are
  processed
• high potential for parallelism

39
Parallel Version 1 use p processors Proci, each
Proci knows centroids C1, C2, ...Ck points are
partitioned (round robin or hashing) into p
groups G1, G2, ... Gp processor Proci processes
group Gi ? parallel k-means has time
complexity 1/p O(nkl)
40
Parallel Version 2 Use GA to generate p different
initial clusterings C1i, C2i, ... , Cki for i
1, 2, ... , p Proci computes solution for the
seed C1i, C2i, ... , Cki and fitness function
for its own solution, which determines the
winning clustering
41

• Large Experiments (main memory)
• classification of lt 40.000 points, basic ideas
• use random sampling to find good initial
  centroids for clustering
• keep summary information in balanced tree
  structures

42
Algorithms for Large Datasets (on disk)

• Divide and conquer cluster subsets of data
  separately, then combine clusters
• Store points on disk, use compact cluster
  representations in main memory, read points from
  disk, assign to cluster, write back with label
• Parallel implementations

43
Ch. 15.7 Nearest Neighbor Clustering Idea every
point belongs to the same cluster as its nearest
neighbor Advantage instead of computing n2
distances in O(n2 ) compute nearest neighbor in O
(nlog(n)) Note this works in 2-dimensional
space with sweep line paradigm and Voronoi
diagrams, unknown complexity in multidimensional
space
44
Nearest Neighbor Clustering Algorithm 1.
Initialize point its own cluster 2. Compute
nearest neighbor Y of X, represent as (X, Y,
dist) O(nlog(n)) for 2 dim expected
O(nlog(n)) for d dim??? I/O complexity
O(n) 3. Sort (X, Y, dist) by dist O
(nlog(n)) 4. Assign point to cluster of
nearest neighbor ( i.g. merge cluster with
nearest cluster and compute new centroid,
diameter, cardinality of cluster, count number of
clusters) 5. if not done then goto 2
45
Termination Criteria

• distance between clusters
• size of clusters
• diameter of cluster
• squared error function
• Analysis with every iteration the number of
  clusters is decreased to at most 1/2 of previous
  number, i.e. at most O( log(n)) iterations,
  total complexity O(nlog2(n))
  resp. O(nlog (n))
• ? we could compute complete dendrogram for
  nearest neighbor clustering!

46
Efficient Computation of Nearest
Neighbor 2-dimensional use sweep line paradigm
and Voronoi diagrams d-dimensional so far just
an idea, try as DA? Use generalization of sweep
line to sweep zone in combination with UB-tree
and caching similar to Tetris algorithm