BEFORE I START MY TALK

1
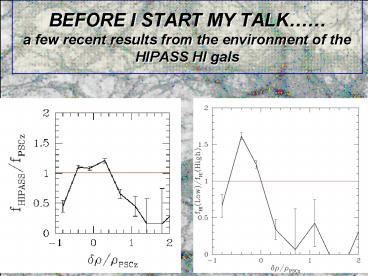
BEFORE I START MY TALK a few recent
results from the environment of the HIPASS HI gals
2
MORPOLOGICAL DYNAMICAL PARAMETERS OF HALOS IN
VOIDS Manolis Plionis (NOA-Greece
INAOE-Mexico)Cinthia Ragone-Figueroa (IATE
Cordoba- Argentina)Amsterdam-Holland, December
2006

• Extension of work taking gas into account is
  under-way using the HR Mare-Nostrum ?CDM
  Simulations
• Gustavo Yepes (Univ. Autonoma de Madrid Spain)
• Stefan Gottlober (Potsdam Univ. Germany)
• Dante Paz (IATE Argentina)
• Nestor Espino Biriones (INAOE, Mexico)

See talks by Porciani et al. and Aragon-Calvo et
al.
3

• What does structure formation paradigm tell us
• CDM-like Power Spectra of initial perturbations
  predict a bottom-up scenario but with roughly
  simultaneous formation of structure at
  large-scales.
• Structures form by gravitational instability
  which as soon as it switches on creates
  anisotropic structures (filaments, walls).
• Galaxies Clusters form in high-density regions
  (inside filaments walls) by anisotropic
  accretion and merging of smaller mass units.
• Roughly simultaneous formation of structure at
  different scales creates cross-talk and thus
  correlated phenomena between these scales

Kaufmann et al 1999
k3/2dk
Log(M/M?)
From West 1994
4
What does formation paradigm tell us
Clusters form by merging accreting matter along
preferred directions (filaments) ? generic in all
hierarchical clustering models, like CDM (cf.
Bardeen et al. 1986 Van Haarlem Van der
Weygaert 1993, Tormen 1997 Knebe et al. 2004),
irrespective of the density parameter for as long
as the spectral index is nlt-1.
Knebe et al 2004
van Haarlem van de Weygaert 1993, West 1994
GADGET Simulations from Yepes, Gottlober, et al.
5
0a. Our simulation, Halo Identification
Procedure Void definition
?CDM simulation Size L500 h-1 Mpc with 5123 DM
particles (mp 7.7 x1010 h-1 Mo) FoF Halo
Identification with linking length l0.17
inter-particle separation Number 58000 haloes
with nmgt130 (Mgt1013 h-1 Mo), 1593 with Mgt2 x 1014
h-1 Mo. Note that we do not identify
independently sub-haloes, that belong to large
haloes (as do for example, Avila-Reese et al.
2005)
Environment Definitions For all Group-size Halos
with 1013ltMlt2x1014 Mo we find the nearest
neighbour distance, Rnn Void Haloes Using as
neighbours all haloes with Mgt1013 Mo we identify
Rnn as the Isolation Radius (Risolation) and
which defines the Void Radius. Haloes near
Clusters Using as neighbours only Cluster haloes
with Mgt2 x1014 Mo) we identify Rnn as the call
Rcluster Radius.
6
0b. Halo Parameter Estimation
Halo density and velocity ellipsoid shapes are
determined by diagonalizing the corresponding
moments of Inertia tensor Alignment between any
two vectors defined as Halo Dynamical state
Dressler Shectman (1998) substructure
?-deviation statistic
7
0c. Halo Parameter Error Estimation
Resolution effects can introduce significant
uncertainties in the derived parameters.
Therefore, we estimate such uncertainties by
selecting the most massive haloes and degrading
them randomly to 130 particles/halo
Systematic errors due to Resolution effects are
also present
8
1. Halo Mass Function in Voids High-density
Regions
Risolationgt12 h-1 Mpc Rcluster lt 4h-1 Mpc
Interesting There are high-mass Group-size halos
which are completely isolated (Risolationgt12h-1Mpc
), corresponding to -0.7ltd?/?lt0.0.
9
2. Morphology of Void High-Density region
Group-size Haloes
Environmental Dependence of the Correlation
between Halo Mass and Shape. Void Halos are
FLATTER more PROLATE and there is smooth
transition as a function of decreasing d?/?.
Shape parameters for Haloes in Voids
(Risolationgt12 h-1 Mpc) and around high density
regions (Rcluster lt 4h-1 Mpc).
Simulation ?CDM Haloes show Mass-flattening
relation (Jing Suto 2002 Allgood et al 2005,
Kasun Evrard 2005, etc)
IMPORTANT This
relation corresponds to an overall
anticorrelation between Mass and c/a of R-0.12
with a random probability of 10-10
The deeper the Void the flatter and the more
prolate the Haloes are.
10
2. Morphology of Void High-Density region
Group-size Haloes
The fact that Void haloes with substructure are
more elongated and prolate than corresponding
haloes in high-density regions, imply that
accretion by anisotropic merging is much more
directional and coherent in Voids.
Dividing haloes in those with high and low
?-deviation index
11
3. Dynamical Characteristics of Void
High-Density region Group-size Haloes
The Virial correlation (M-s) is respected in
Voids but NOT near Clusters. This implies that
the measured velocity dispersion of observed
groups in the vicinity of Clusters is an
unreliable measure of there Mass.
The observed correlation around massive haloes is
not due to s-? virial correlation. The s-? virial
correlation is respected in Voids.
Ragone-Figueroa et al 2004 Halo velocity
dispersion dependence on distance from massive
host.
The Halo s is lower in Voids (Risolationgt12 h-1
Mpc) with respect to high density regions
(Rcluster lt 4h-1 Mpc) for equal mass haloes (lt4
x 1013 Mo). The angular momentum is larger in
high-density regions, independent of halo mass.
12
3. Dynamical Characteristics of Void
High-Density region Group-size Haloes
The fact that the substructured Haloes are those
for which the M-s correlation breaks near
Clusters implies that the cause is probably
contamination of s by bulk (infall) motions of
sub-haloes
Dividing haloes in those with high and low
?-deviation index
13
4. Alignments of Void High-Density region
Group-size Haloes
Void Haloes are more aligned with their nearest
neighbour, with respect to haloes in high-density
regions. The coherence of the Void Halo alignment
extends to large distances. This again supports
that accretion by anisotropic merging is much
more directional and coherent in Voids.
Alignments of nearest-neighbour cluster group
size haloes is well known (eg. Splinter et al.
1997, Onuora Thomas 2000, Faltenbacher et al.
2002, Kasun Evrard 2005, Hopkins et al. 2005,
Basilakos et al. 2006).
14
4. Alignments of Void High-Density region
Group-size Haloes
Dividing haloes in those with high and low
?-deviation index
15
5. Clustering of Halos as a function of level
of substructure
2-p spatial correlation analysis shows that
dynamically young Halos are more clustered than
virialized ones ie., they are found in
high-density regions.
Dynamically young (high ?) Halos are more
clustered (found in high-density environments!
(as expected from mass function of different ?
???? depending on environment
Espino-Briones, Plionis Ragone-Figueroa, 2007
APM clusters (Plionis Basilakos 2002)
16
Conclusions
1. There are high-mass Group-size halos which are
completely isolated (Risolationgt12h-1Mpc),
corresponding to -0.7ltd?/?lt0.0. 2. Environmental
Dependence of the correlation between group-size
Halo Mass and Shape. (a) Void Halos are more
ELONGATED more PROLATE, and there is smooth
transition as a function of decreasing d?/?. (b)
Substructured Void haloes are more elongated and
more prolate than corresponding haloes in
high-density regions, which imply that accretion
by anisotropic merging is much more directional
and coherent in Voids. 3. Void Haloes are more
aligned with their nearest neighbour, with
respect to haloes in high-density regions. The
coherence of the Void Halo alignment extends to
large distances. This again supports that
accretion by anisotropic merging is much more
directional and coherent in Voids. 4. The Virial
correlation (M-s) is respected for Halos in Voids
but NOT near Clusters. (a) This implies that the
measured velocity dispersion of observed groups
in the vicinity of Clusters is an unreliable
measure of their Mass (CAUTION OBSERVERS !), (b)
The fact that the substructured Haloes are those
for which the M-s correlation breaks near
Clusters implies that the cause is probably
contamination of s by bulk (infall) motions.
RELATED TALKS by C. PORCIANI et al. M.
ARAGON-CALVO et al.