Physics of LIGO

1
Physics of LIGO
2
Warped space-time Einsteins General Relativity
(1916)
We envision gravity as a curvature of space as a
massive body moves, the curvature changes with it.
Einsteins theory tells us that this information
will be carried by gravitational radiation at the
speed of light.
3
AstrophysicalSources of Gravitational Waves
Coalescing compact binaries (neutron stars, black
holes)
Non-axi-symmetric supernova collapse
Non-axi-symmetric pulsar (rotating, beaming
neutron star)
4
Studying strong-field GR with gravitational waves
Compact binary mergers
We can use (weak-field) gravitational waves to
study strong-field general relativity, where GR
gets nonlinear and interesting!
5
Why are we so confident? Hulse-Taylor binary
pulsar
6
Nature of Gravitational Radiation

• General Relativity predicts
• transverse space-time distortions, freely
  propagating at speed of light
• expressed as a strain (?h ?L/L)
• Conservation laws
• conservation of energy ? no monopole
  radiation
• conservation of momentum ? no dipole radiation
• quadrupole wave (spin 2) ? two polarizations
• plus (?) and cross (?)

7
Magnitude of GW strain

• Accelerating charge ? electromagnetic radiation
• Accelerating mass ? gravitational radiation
• Amplitude of the gravitational wave (dimensional
  analysis)
• second derivative
• of mass quadrupole moment
• (non-spherical part of
• kinetic energy)
• G is a small number!
• Need huge mass, relativistic
• velocities, nearby.
• For a binary neutron star pair,
• 10m light-years away, solar masses
• moving at 15 of speed of light

8
Thats REALLY small!
L 1.5 1011 m
Sun
Earth
?L 10-10 m
h 10-21 is equivalent to the distance from the
Earth to the Sun changing by the width of an atom!
9
Can we generate gravitational waves?
Imagine if we put two 1-ton masses on the ends of
a 2-meter long bar, and spun the bar at 100 Hz
(!?!). If our detector is next to this setup
2m
103 kg
103 kg
M 103 kg R 1 m F 100 Hz r 1 m
10-36 !!
Terrestrial sources are TOO WEAK!
10
First AttemptResonant Bar Detectors
In 1966 Joseph Weber constructed the first
resonant-bar gravitational wave detector. By
1969 the detector had reached a strain
sensitivity of h 10-16. The detector consisted
of an aluminum bar suspended in a vacuum chamber.
A passing gravity wave would stretch or contract
the bar, generating heat that would cause the bar
to ring at its resonant frequency. Such a
detector has two problems, both related to the
fact that it can sense only one frequency

• Cannot determine shape of gravitational wave
• Noise looks exactly the same as signal

GW wave
Aluminum bar
11
The Michelson-Morley experiment
12
Application of Michelson interferometer
The Michelson interferometers shape is perfectly
suited to the quadrupole nature of gravitational
radiation. In addition, Michelson and Morley
could measure 1/100th of a fringe with 1900s
technology. With high-power lasers and modern
photodiodes, we can do far better.
13
How sensitive is an interferometer?
Imagine a high-powered NdYAG laser (? 1.064
µm) in an interferometer with 5 km arms (longest
curvature of Earth will allow) ?L/L
(?laser)/(length of arms) (10-6 m)/(10 km)
10-10, not even close!
Michelson and Morley didnt build 11m arms,
though (thats a lot of mercury!). They folded
the light path several times with nearly parallel
mirrors. But we dont have room or money for
thousands of mirrors!
14
Folding the arms two methods
Delay line simpler, but requires large mirrors to
prevent crosstalk limited storage
time. Fabry-Perot more compact, storage time in
msec, but harder to control.
For one fringe, ?L/L (?laser)/(length of arms
folding) (10-6
m)/(10 km 1000) 10-13 With enough laser
power, measuring 10-8 of a fringe can be done!
15
The LIGO Project

• LIGO Laser Interferometer Gravitational-Wave
  Observatory
• US project to build observatories for
  gravitational waves (GWs)
• to enable an initial detection, then an astronomy
  of GWs
• collaboration by MIT, Caltech other institutions
  participating
• (LIGO Scientific Collaboration, LSC)
• Funded by the US National Science Foundation
  (NSF)
• Observatory characteristics
• Two sites separated by 3000 km
• each site carries 4km vacuum system,
  infrastructure
• each site capable of multiple interferometers
  (IFOs)
• Evolution of interferometers in LIGO
• establishment of a network with other
  interferometers
• A facility for a variety of GW searches
• lifetime of gt20 years
• goal best technology, to achieve fundamental
  noise limits for terrestrial IFOs

16
The LIGO sites
LIGO Hanford Observatory (LHO)
LIGO Livingston Observatory (LLO)
17
International network
Simultaneously detect signal (within msec)
GEO
Virgo
LIGO
TAMA

• detection confidence
• locate the sources
• verify light speed propagation
• decompose the polarization of gravitational
  waves

AIGO
18
How does the LIGO interferometer work?

• The concept is to compare the time it takes light
  to travel in two orthogonal directions transverse
  to the gravitational waves.
• The gravitational wave causes the time difference
  to vary by stretching one arm and compressing the
  other.
• The interference pattern is measured (or the
  fringe is split) to one part in 1010, in order to
  obtain the required sensitivity.

19
Power recycling

• The interferometer is run as a null instrument
  the arm lengths are set such that no light is
  output
• When a gravitational wave passes, the arm lengths
  change and light exits the dark port
• More laser power more sensitivity, but the
  power is being wasted out the bright port!
• Add a power recycling mirror at the bright port,
  making a resonant compound cavity to dump the
  light back in

bright port
dark port (GW signal)
20
Suspended test masses

• To respond to the gravitational wave, test
  masses (mirrors) must be free falling
• The Earth is vibrating like mad at low
  frequencies (seismic, thermal, acoustic,
  electrical)
• cant simply bolt the masses to the table
• Mirrors suspended on a pendulum with f0 1 Hz
• fixed against gravity at low frequencies, but
• free to move at frequencies above 100 Hz

Free mass pendulum at
21
Length Sensing and Control (LSC)

• Each optic has five OSEMs (magnet and coil
  assemblies), four on the back, one on the side

• The magnet occludes light from the LED, giving
  position
• Current through the coil creates a magnetic
  field, allowing mirror control

22
Two problems

• If we are operating at the dark fringe, we are
  at the base of a sine wave in power, and a large
  phase shift will cause a small change in the
  output light. How can we make our interferometer
  more sensitive?

intensity shift
phase shift

• The arm lengths have to be kept in resonance to a
  fraction of a micron, but the mirrors are
  swinging! How do we sense and control the
  lengths of the arm cavities?

23
Cavity control

• Pound-Drever (reflection) locking used to control
  lengths of all the optical cavities in LIGO
• Phase modulate incoming laser light, producing
  RF sidebands
• Carrier is resonant in cavity, sidebands are not
• Beats between carrier and sidebands provide
  error signal for cavity length

24
Demodulation
Modulated light A cos (wt) B cos (w wm)t
B cos (w wm)t Power A2 AB cos (wmt)
B2 cos (2wmt)
If we multiply the power by our modulation
frequency in an electronic mixer and average over
several cycles, only the AB cos (wmt) term
will remain. But this term is linear in A, which
is the amplitude of the signal in the arms. We
now have a correction signal for our length
controls, and a linearly-sensitive signal for
gravitational waves.
25
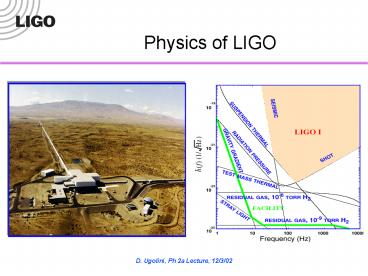
Predicted LIGO sensitivity

• Sensitivity expressed as a function of frequency
• Optimal sensitivity from 100-300 Hz
• Too high for most stochastic sources
• Corresponds to last 1/100th of a second of
  inspiral
• Many pulsars rotate in the hundreds of Hz

26
Seismic isolation stacks
27
Thermal noise

• Thermal noise comes primarily from
• Vibration of the atoms in the test masses
• Violin modes of the suspension wire
• Cannot get rid of it!
• Thermal noise kT
• Vacuum conducts heat poorly
• Cannot cool mirrors without
  seismic short
• Vibration confined to
  normal modes

28
Fluctuation-dissipation theorem
The narrowness of the normal mode resonance
peak in frequency is described by the quality
factor, or Q value of the mode.
The larger the Q value, the less energy that
leaks into other frequencies in the form of
noise. This is called the fluctuation-dissipation
theorem. So we design our supports and mirrors
to have normal modes with high f and Q.
29
LIGO Science Run (S1)Strain Sensitivities
LIGO S1 Run ----------- First Upper Limit
Run Aug Sept 02
Total time with all three IFOs in lock 138
hours Duty cycle 36
30
We need Advanced LIGO!

• X10 in sensitivity x1000 volume searched
• LIGO 0.3-3 inspirals/year
• Adv. LIGO 300-3000 inspirals/year
• Factor of ten improvement needed at all
  frequencies

31
The signal recycling mirror
We add a signal recycling mirror (SM) at the
asymmetric output port. This forms a compound
mirror with the input test masses (ITMs) with
reflectivity
with f kls 2pls(fcarrfsig)/c
32
The Caltech 40m Prototype
The 40m is a controls and engineering prototype
for signal recycling, and a testbed for Advanced
LIGO innovations.
33
LIGO III -- Cryogenics
The Large-scale Cryogenic Gravitational-wave
Telescope (LGCT) in Japan will link test masses
to a liquid helium tank through sapphire fibers
and metal springs.
34
The polarization Sagnac IFO

• All reflective optics to minimize thermal
  distortions
• Common path for interfering beams
• Grating beam splitter (double-pass, to null
  dispersion)
• Delay line arms
• Heroic efforts to minimize noise due to scattered
  light
• Polarization allows the light to exit the IFO at
  the symmetric port of the beam splitter
• Many clever tricks to ensure robust control, low
  noise

35
The Laser Interferometer Space AntennaLISA
The center of the triangle formation will be in
the ecliptic plane 1 AU from the Sun and 20
degrees behind the Earth.
Three spacecraft in orbit about the sun,
with 5 million km baseline
36
LISA orbit
The orbit of the triangle of spacecraft tumbles
as it orbits the sun, to be sensitive to all
directions in the sky, and to even out the
thermal load (from the sun) on the three
spacecraft.
37
LISA Spacecraft