El problema del transporte: Definicin

1
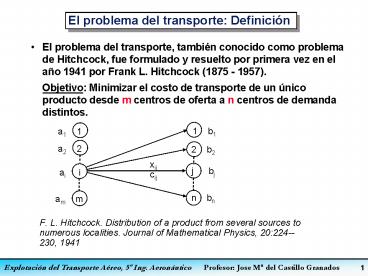
El problema del transporte Definición

• El problema del transporte, también conocido como
  problema de Hitchcock, fue formulado y resuelto
  por primera vez en el año 1941 por Frank L.
  Hitchcock (1875 - 1957).
• Objetivo Minimizar el costo de transporte de un
  único producto desde m centros de oferta a n
  centros de demanda distintos.

1 b1
2 b2
xij
j bj
ai i
cij
n bn
am m

• F. L. Hitchcock. Distribution of a product from
  several sources to numerous localities. Journal
  of Mathematical Physics, 20224--230, 1941

2
El problema del transporte Definición

• m número de centros (orígenes) distintos
• n número de destinos distintos
• cijcosto unitario de transporte del origen i al
  destino j
• xijvolumen de unidades del uno al otro
• aioferta
• bjdemanda

3
El problema del transporte Definición

• Sumando las restricciones de oferta y las de
  demanda por separado, se tiene
• Por tanto

• Para que este problema tenga solución hay que
  verificar que el volumen ofertado siempre es
  superior que la demanda. Es decir

4
El problema del transporte Formulación

• Hipótesis la oferta coincide con la demanda en
  el problema del transporte

5
El problema del transporte Formulación
El problema puede ahora escribirse en forma
matricial Minimizar cx s.a. Axb
x 0 donde x(x11,x12,...,x1n,x21,..
.,xmn)T c(c11,c12,...,c1n,c21,...,cmn)T b(a1,a
2,...,am,b1,b2,...,bn)T
6
Problema dual
Problema dual
Problema primal

• El problema dual constará de m x n ecuaciones
  con mn incógnitas. Por los teoremas de holgura
  se sabe
• si xij es básica ?uiujcij
• si xij es no básica ?uiujltcij
• Optimo cuando los costos relativos de las
  variables no básicas del problema sean todos no
  negativos rij cij-(uiuj)

7
La tabla del problema del transporte
Una columna por cada centro de demanda
a1
Una fila por cada centro de oferta
ai
am
b1
bj
bn
En cada celda el costo del transporte
8
La tabla del problema del transporte ciclos

• De las m n celdas definidas, solo mn-1 pueden
  encontrarse a un nivel no nulo (es decir mn-1
  variables básicas).
• Se denomina por ciclo a toda secuencia ordenada
  de cuatro a mas celdas con los siguientes
  propiedades
• dos celdas consecutivas se encuentran en la misma
  fila o columna.
• nunca más de dos celdas consecutivas en la misma
  fila o columna.
• Ejemplos

no válidas
9
Algoritmo del PDT
Problema dual
Problema primal

• El problema dual constará de m x n ecuaciones
  con mn incógnitas. Por los teoremas de holgura
  se sabe
• si xij es básica ?uivjcij
• si xij es no básica ?uivjltcij
• Optimo cuando los costos relativos de las
  variables no básicas del problema sean todos no
  negativos rij cij-(uivj)

10
Algoritmo del PDT

• Como el número de variables básicas del problema
  primal es mn-1, el número de ecuaciones del
  problema dual que debe verificarse con estricto
  signo de igualdad debe ser también mn-1, y como
  el número de variables duales que tenemos es mn,
  una de ellas tiene que ser definida
  arbitrariamente.
• El costo relativo más negativo determinará el
  criterio de la variable que entra en la base.
• Una vez determinada la variable y su celda
  asociada que entra en la base, se determina el
  ciclo que forma con las variables básicas.
• En este ciclo, las celdas básicas definen sus
  esquinas, que tendrán asignadas signo ó
  alternativos.
• Para que los niveles de oferta y demanda se
  mantengan constante, el nivel de la celda no
  básica tendrá que incrementarse, como máximo en
  el mínimo valor del nivel de la celda básica
  marcada con signo -, pasando esta última celda a
  ser no básica.
• las celdas marcadas con incrementarán su nivel
  en la misma cantidad que las celdas marcados con
  signo lo decrementarán.

11
Algoritmo del PDT

• Calcular variables duales y costes relativos
• Encontrar la variable que entra en la base
• Seleccionar la variable que sale de la base.
• Calcular variables duales y costes relativos
• Si existe un rijlt0 volver a II.

12
Algoritmo del PDT 3

• Encontrar la variable que entra en la base
• Resolver el sistema de ecuaciones duales
  correspondientes a la mn-1 variables básicas.
  Como el número de ecuaciones es mn-1 y el de
  incógnitas duales mn, se define una de ellas a
  nivel cero y se obtienen los valores de las
  restantes resolviendo
• Obtener, para todas las variables no básicas, los
  costos relativos
• si éstos son positivos se ha alcanzado el
  optimo, en caso contrario ir a I-c.
• La variable que entra en la base xkl, celda
  (k,l), será aquella con costo relativo negativo
  menor.
• Seleccionar la variable que sale de la base.
• Volver a I.

13
Algoritmo del PDT 3

• Encontrar la variable que entra en la base
• Seleccionar la variable que sale de la base.
• Identificar el ciclo formado por la variable que
  entra en la base y las variables básicas.
• Marcar con signo y alternativos las esquinas
  del ciclo, comenzando con el signo para la
  nueva celda básica.
• De entre todas las celdas marcadas con signo ,
  elegir aquella celda con variable de menor valor.
  Este valor definirá el incremento ?.
• Incrementar todas las celdas marcadas con en ?,
  decrementanto todas las celdas marcadas con en
  ?.
• La variable que deja de ser básica se encontrará
  ahora a nivel nulo.
• Volver a I.

14
Exceso de Oferta

• Las restricciones tienen la forma
• para convertirlo en forma estandar se define un
  destino artificial n1 ésimo y las variables de
  holgura xi,n1

15
Exceso de Oferta
Adicionando las restricciones de oferta y demanda
y de ambas
siendo bn1 la demanda de este destino ficticio.
16
Exceso de Oferta
La formulación del problema quedará como

• m número de centros de producción distintos
• n número de destinos distintos
• cijcosto unitario de transporte del origen i al
  destino j
• xijvolumen de unidades del uno al otro
• aioferta
• bjdemanda

donde ci,n1 serán nulos o tendrán un cierto
valor debido a un costo de almacenamiento
17
Ejemplo Exceso de Oferta
8
4
5
4
18
Ejemplo Exceso de Oferta
8
Total Oferta 12
4
5
4
Exceso de Oferta 12-93
Total Demanda 9
19
Ejemplo Exceso de Oferta
8
4
3
5
4
20
Exceso de Demanda

• Las restricciones tienen la forma
• para convertirlo en forma estándar se define un
  origen artificial m1 ésimo y las variables de
  holgura xm1,j

21
Exceso de Demanda
Adicionando las restricciones de oferta y demanda
y de ambas
siendo am1 la oferta de este origen ficticio.
22
Exceso de Demanda
Los costos que implican a este origen virtual
serán cm1,j0. La formulación del problema
quedará como

• m número de centros de producción distintos
• n número de destinos distintos
• cijcosto unitario de transporte del origen i al
  destino j
• xijvolumen de unidades del uno al otro
• aioferta
• bjdemanda

23
Ejemplo Exceso de Demanda
5
6
4
14
24
Ejemplo Exceso de demanda
5
Total Oferta 11
6
4
14
Exceso de Demanda 18-117
Total Demanda 18
25
Ejemplo Exceso de Demanda
5
6
7
4
14
26
Exceso de Oferta
Los costos que implican a este origen virtual
serán cm1,j0. La formulación del problema
quedará como

• m número de centros de producción distintos
• n número de destinos distintos
• cijcosto unitario de transporte del origen i al
  destino j
• xijvolumen de unidades del uno al otro
• aioferta
• bjdemanda

27

• Rutas prohibidas

28
Rutas prohibidas

• En algunos problemas es imposible hacer algunos
  rutas origen/destino
• Para poder usar el mismo algoritmo ? asignar un
  costo absoluto muy elevado (M)
• El optimo no va a aparecer como básicas.
• Método de las dos fases
• Considerando toda las rutas se obtiene una
  solución básica.
• Si la solución no implica asignación en celda
  prohibida?admisible, tachar las celdas prohibidas
  se resuelve el problema
• Si la solución inicial implica asignación en
  celda prohibida aplicar fase I.
• Fase I asignar costos absolutos unidad en celdas
  prohibidas nulos en los demás. Resolver y obtener
  una solución básica inicial.
• Si esta solución básica no implica celdas
  prohibidas?tachar celdas prohibidas y usar costos
  absolutos originales para obtener SBF.
• Si esta solución implica celdas prohibidas? no
  tiene SBF.

29
Rutas prohibidas Ejemplo
Obtener la solución optima de un problema del
transporte definido por
Costo unitario de transporte
Volumen de oferta
Volumen de demanda
30
Rutas prohibidas Ejemplo
Se puede aplicar penalización o el método de la
Fase I, probamos el ultimo celdas permitidas
? costo nulo celda prohibida ? costo unidad
10
70
20
50
Solución inicial
Aplicando método Vogel
31
Rutas prohibidas Ejemplo
Fase II tachar celdas prohibidas y usando costos
originales.
-

Costos relativos

-
u1v19 ? v19 u1v23 ? v23 u2v25 ?
u22 u2v32 ? v30 u2v410 ? v48
32
Rutas prohibidas Ejemplo

-

-
Todo los costos relativos positivos ? Óptimo

-
u1v19 ? v19 u1v47 ? v47 u2v25 ?
u23 u2v32 ? v3-1 u2v410 ? v22

-
Costos relativos
33

• Degeneración

34
Degeneración

• Se produce degeneracion en un problema del
  transporte cuando al iniciar el proceso
  iterativo, o en cualquier otro paso, un
  subconjunto de las ofertas iguala a un
  subconjunto de las demandas.
• Dos casos distintos
• Una oferta coincide con una demanda y al asignar
  el nivel correspondiente a las celda, ambas se
  satisfacen simultáneamente.
• Una oferta modificada coincide con una demanda
  modificada. Ambas se satisfarán simultáneamente
  si la celda es básica.
• Se soluciona el problema de degeneración
  arrastrando una variable a nivel cero.

35
Degeneración ejemplo
20 30 40
10 10 20
50
36
Degeneración ejemplo
Dif.
Menor costo
20 1 30 4 40 6
10
Método de Vogel
10 10 20
50
Diferencia entre los dos costos más pequeños
Dif 10 9 1
2
Major Dif.
37
Degeneración ejemplo
Menor costo
Dif.
10 1 30 4 40 6
0
Método de Vogel
10 10 20
50
Dif 10 9 1
2
Major Dif.
La oferta coincide con la demanda y al asignar
el nivel correspondiente a las celda, ambas se
satisfacen simultáneamente.
38
Degeneración ejemplo
Menor costo
Dif.
10 1 30 4 40 6
10
Método de Vogel
10 10 20
50
Dif 10 3 4
2
Major Dif.
39
Degeneración ejemplo
Menor costo
Dif.
10 1 10 - 40 -
Método de Vogel
40
10 10 20
50
Dif 10 3 4
2
Major Dif.
40
Degeneración ejemplo
Hemos alcanzado una solución básica inicial
compuesta de 5 variables básicas. mn-16 pero
solo existen 5 celdas asignadas, el grado de
degeneración es 1 ?es necesario definir una
variable básica degenerada a nivel nulo. Elegir
como variable degenerada la asociación a aquella
celda con menor costo absoluto y que no defina un
ciclo con el resto de las variables básicas.
41
Degeneración ejemplo
9
4
3
2
9
10
10
0
0
0
0
1
5
12
14
10
20
8
11
0
0
3
9
15
12
40
2
0
9
7
Costos relativos
Las ecuaciones duales
u1v12 u1v23 u1v34 u2v35 u2v41 u3v43
Todo los costos son positivos, o sea se ha
alcanzado el óptimo
42
Aspectos computacionales

• Método Hitchcock mucho más eficiente que Simplex
• Solo se suma o resta. En Simplex hay que
  multiplicar, dividir. ? Una orden de magnitud más
  lento.
• Tamaño
• Hitchcock mxn
• Simplex mn-1 filas x mxn columnas
• En el problema de Hitchcoch se puede convertir
  todo en enteros
• Más rápido
• No hay errores de redondeo

43
Problema del transbordo
1 b1
2 b2
xij
j bj
ai i
cij
D
O
1 m 1 n
n bn
am m
a1d amd d bn
1 m 1 n
O
D
b1 bn
d d d d
44
Problema del transbordo
9
1
12
20
2
6
10
3
A
2
9
3
10
6
B
14
5
7
3
9
1 2 3
A B
2027 7 27 27 27 27
27 27 927 927 927