IP: Addresses and Forwarding

1
(No Transcript)
2
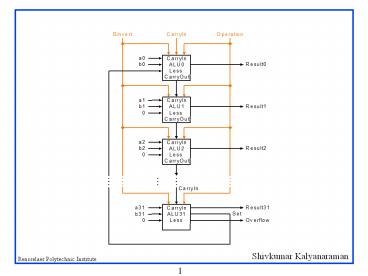
Problem ripple carry adder is slow

• Is a 32-bit ALU as fast as a 1-bit ALU?
• Is there more than one way to do addition?
• Two extremes ripple carry and sum-of-products
• c1 b0c0 a0c0 a0b0
• c2 b1c1 a1c1 a1b1
• c3 b2c2 a2c2 a2b2
• c4 b3c3 a3c3 a3b3

3
Carry-lookahead adder

• An approach in-between our two extremes
• More complexity (gates) vs less propagation
  (levels)
• Motivation
• If we didn't know the value of carry-in, what
  could we do?
• When would we always generate a carry? gi
  ai bi
• When would we propagate the carry? pi
  ai bi
• Rewriting the carry equations, we get
• c1 g0 p0c0
• c2 g1 p1c1 or c2
• c3 g2 p2c2 or c3
• c4 g3 p3c3 or c4

4
Carry-lookahead adder block

• Consider the equation for the last carry c4
• c4 g3 (p3.g2) (p3.p2.g1) (p3.p2.p1.g0)
• (p3.p2.p1.p0.c0), or .
• c4 G0 P0.c0, where
• G0 g3 (p3.g2) (p3.p2.g1) (p3.p2.p1.g0)
• P0 p3.p2.p1.p0
• Calling c4 as C1 and c0 as C0, we have C1 G0
  P0.C0

5
Use principle to build bigger adders

• Use 4-bit ALU and a 4-bit CLA building blocks
• I.e., given Pi, Gi and C0, 4-bit CLA can find C1,
  C2, C3, C4 in parallel!
• Ripple is eliminated !
• Ripple carry speed
• (16 hops between 1-bit ALUs)
• (2 logic levels at each ALU)
• 32 gate delays
• CLA-adder speed
• (1 logic level to compute pi, gi)
• (2 logic levels to compute Pi, Gi from pi,gi)
• (2 logic levels at CLA to compute Ci)
• 5 gate delays !!

C
a
r
r
y
I
n
a
0
C
a
r
r
y
I
n
b
0
R
e
s
u
l
t
0
-
-
3
a
1
b
1
A
L
U
0
a
2
p
i
P
0
4-bit
b
2
g
i
G
0
a
3
b
3
C
a
r
r
y
-
l
o
o
k
a
h
e
a
d

u
n
i
t
C
1
c
i



1
C
a
r
r
y
I
n
a
4
b
4
R
e
s
u
l
t
4
-
-
7
a
5
b
5
A
L
U
1
a
6
p
i



1
P
1
b
6
g
i



1
G
1
a
7
b
7
C
2
c
i



2
C
a
r
r
y
I
n
a
8
b
8
R
e
s
u
l
t
8
-
-
1
1
a
9
b
9
A
L
U
2
a
1
0
p
i



2
P
2
b
1
0
G
2
g
i



2
a
1
1
b
1
1
C
3
c
i



3
C
a
r
r
y
I
n
a
1
2
b
1
2
R
e
s
u
l
t
1
2
-
-
1
5
a
1
3
b
1
3
A
L
U
3
a
1
4
p
i



3
P
3
g
i



3
G
3
b
1
4
a
1
5
C
4
c
i



4
b
1
5
C
a
r
r
y
O
u
t