1D%20Pulse%20sequences - PowerPoint PPT Presentation
Title:
1D%20Pulse%20sequences
Description:
The simplest one, the sequence to. record a normal 1D spectrum, will ... According to the direction of the pulse, ... CH (a methine carbon). After the p ... – PowerPoint PPT presentation
Number of Views:52
Avg rating:3.0/5.0
Title: 1D%20Pulse%20sequences
1
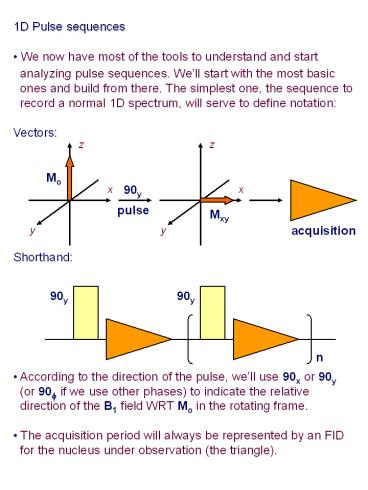
- 1D Pulse sequences
- We now have most of the tools to understand and
start - analyzing pulse sequences. Well start with the
most basic - ones and build from there. The simplest one,
the sequence to - record a normal 1D spectrum, will serve to
define notation - Vectors
- Shorthand
z
z
Mo
x
x
90y
pulse
Mxy
y
y
acquisition
90y
90y
n
2
- Inversion recovery
- Measurement of T1 is important, as the
relaxation rate of - different nuclei in a molecule can tell us
about their local - mobility. We cannot measure it directly on the
signal or the - FID because T1 affects magnetization we dont
detect. - We use the following pulse sequence
- If we analyze after the p pulse
180y (or x)
90y
tD
z
z
180y (or x)
x
x
tD
y
y
3
- Inversion recovery (continued)
tD 0
z
z
x
x
90y
FT
y
y
tD gt 0
z
z
x
x
90y
FT
y
y
tD gtgt 0
z
z
x
x
90y
FT
y
y
4
Inversion recovery (continued)
at 40oC
- If we plot intensity versus time (td),
- we get the following
I(t) I? ( 1 - 2 e - t / T1 )
Intensity ( )
time
5
- Spin echoes
- In principle, to measure T2 we would only need
to compute - the envelope of the FID (or peak width),
because the signal - on Mxy, in theory, decays only due to
transverse relaxation. - The problem is that the decay we see on Mxy is
not only due - to relaxation, but also due to inhomogeneities
on Bo (the - dephasing of the signal). The decay constant we
see on the - FID is called T2. To measure T2 properly we
need to use - spin echoes.
- The pulse sequence looks like this
180y (or x)
90y
tD
tD
6
- Spin echoes (continued)
- We do the analysis after the 90y pulse
z
y
y
tD
x
?
x
x
y
dephasing
y
y
tD
x
x
180y (or x)
refocusing
z
y
?
x
y
7
- Spin echoes (continued)
- If we acquire an FID right after the echo, the
intensity of the - signal after FT will affected only by T2
relaxation and not by - dephasing due to an inhomogeneous Bo. We repeat
this for - different tDs and plot the intensity against 2
tD. In this case - its a simple exponential decay, and fitting
gives us T2.
at 90oC
Intensity ( )
I(t) Io e - t / T2
time
8
- Applications of spin echo sequences
- So far we havent discussed how chemical shift
and coupling - constants behave during spin echos. Here well
start seeing - how useful they are...
- A pretty anoying thing we have to do in NMR
spectroscopy is - phase the spectrum. Why do we have to do this?
We have to - think on the effects of chemical shift on
different components - of Mxy during a short time or delay.
- This short delay, called the pre-acquisition
delay (DE), is - needed or otherwise the remants of the high
power pulse - will give us artifacts in the spectrum or burn
the receivers.
y
y
...
?
x
x
9
- Spectrum phasing
- The phase of the lines appears due to the
contribution of - absorptive or real (cosines) and dispersive or
imaginary - (sines) components of the FID. Depending on the
relative - frequencies of the lines, well have more or
less sine/cosine - components
- S(w)x S cosines(w) - real
spectrum - S(w)y S sines(w) - imaginary
spectrum - What we want is the purely absorptive spectrum,
so we - combine different amounts of the real (cosine)
and the - imaginary (sine) signals obtained by the
detector. The - combination depends on the frequency of the
spectrum
10
- Spin-echoes on chemical shift
- Now we go back to our spin-echoes. The effects
on elements - of Mxy with an offset from the B1 frequency are
analogous to - those seen for dephased Mxy after the p / 2
pulse - After a time tD, the magnetization precesses in
the ltxygt - plane weff tD (f) radians, were weff w -
wo. After the p pulse - and a second period tD, the magnetization
precesses the - same amount back to the x axis.
z
y
y
tD
x
?
x
x
f
y
weff
y
y
180
tD
x
?
x
f
weff
11
- Spin-echoes and heteronuclear coupling
- We now start looking at more interesting cases.
Consider a - 13C nuclei coupled to a 1H
- If we took the 13C spectrum we would see the
lines split due - to coupling to 1H. The 1JCH couplings are from
50 to 250 Hz, - and make the spectrum really complicated and
overlapped. - We usually decouple the 1H, which means that we
saturate - 1H transitions. The 13C multiplets are now
single lines
J (Hz)
bCbH
13C
aCbH
1H
1H
bCaH
I
13C
aCaH
bCbH
13C
aCbH
1H
1H
bCaH
13C
I
aCaH
12
- Spin-echoes and heteronuclear coupling ()
- We modify a little our pulse sequence to include
decoupling - Now we analyze what this combination of pulses
will do to - the 13C magnetization in different cases. We
first consider a - CH (a methine carbon). After the p / 2 pulse,
we will have - the 13C Mxy evolving under the action of J
coupling. Each
180y (or x)
90y
tD
tD
13C
1H
1H
z
y
y
- J / 2
(a)
tD
?
x
x
f
x
y
(b)
J / 2
13
- Spin-echoes and heteronuclear coupling ()
- We now apply the p pulse, which inverts the
magnetization, - and start decoupling 1H. This removes the
labels of the two - vectors, and effectively stops them. They
collapse into one, - with opposing components canceling out
- In this case the second tD under decoupling of
1H is there to - refocus chemical shift and get nice phasing
- Now, if we take different spectra for several tD
values and plot
y
y
y
?
?
x
x
x
tD 1 / 2J
tD 1 / J
tD
14
- Spin-echoes and heteronuclear coupling ()
- The signal intensity varies with the cosine of
tD, is zero for tD - values equal to multiples of 1 / 2J and
maximum/minimum - for multiples of 1 / J.
- If we are looking at a CH2 (methylene), the
analysis is - similar, and we obtain the following plot of
amplitudes versus - delay times
tD 1 / 2J
tD
tD 1 / J
tD 1 / 2J
tD 1 / J
tD
15
- Spin-echoes and heteronuclear coupling ()
- Now, if we make the assumption that all 1JCH
couplings - are more or less the same (true to a certain
degree), and - use the pulse sequence on the following
molecule with a tD - of 1 / J, we get (dont take the d values for
granted)
5
3
7
2
4
6
6
1
1,4
0 ppm
150
100
50
5
2,3
7
16
- Spin-echoes and homonulcear coupling
- Here well see why spin echoes wont work if we
want to get - our perfectly phased spectrum. The problem is
that so far we - have only used single lines (no homonuclear J
coupling) or - systems that have heteronuclear coupling.
- Lets consider a 1H that is coupled to another
1H, and that we - are exactly on resonance. After the p / 2 pulse
of the spin- - echo sequence and the td delay we have
evolution under the - effects of J coupling. Each vector will be
labeled by the state - of the 1H it is coupled to. We have
z
J / 2
y
y
(a)
tD
?
x
x
x
y
(b)
J / 2
17
- Spin-echoes and homonulcear coupling ()
- The p pulse flips the vectors and inverts the
labels - Now, instead of refocusing, things start moving
backwards, - and we will have even more separation of the
lines of the - multiplet during the second evolution period.
If we then take - the FID, the signal will be completely
dispersive (although - this depends on the length of the tD periods)
J / 2
J / 2
y
y
(a)
(b)
180y (or x)
x
x
(b)
(a)
J / 2
J / 2
y
tD
FID, FT
x
18
- Spin-echoes and homonulcear coupling ()
- We see why this is not all that useful. For
different td values - we get the following lineshapes for a doublet
coupled with - a triplet (both have the same J value)
19
- Binomial pulses
- Binomial pulses are examples of pulse trains
which we can - explain with vectors. Among other things, we
can use them - to eliminate solvent peaks (see T1).
- The simplest binomial pulse is the 11, two p /
2 pulses with - opposite signs, separated by a certain interval
td, and exactly - on resonance with the peak we want to
eliminate - The first p / 2 puts everything on ltxygt. After
td, signals/spins - precess to one side or the other of x. All
except the signal we
z
z
y
Mo
90y
tD
x
x
x
y
y
20
- Binomial pulses (continued)
- The next p / 2 return everything on x to the z
axis. This - includes all the signal corresponding to the
peak to eliminate, - as well as the x components of the remaining
signals - The resulting FID only has signals corresponding
to peaks - that arent in resonance with the carrier. They
will all be in - phase with the receiver, but signals on each
side of the - carrier will have opposite signs
y
y
90-y
?
x
x
x
y
y
FID (y) FT
x
21
- Binomial pulses ()
- As mentioned before, they are used to eliminate
solvent - peaks, particularly water in cases that other
secuences could - perturb protons that exchange with water (NHs,
OHs, etc.). - 50 mM sucrose in H2O/D2O (9 to 1).
- 1H spectrum
22
- Binomial pulses ()
- To avoid the sign change we can use other
binomial pulse - trains, such as the 1331
- You also get artifacts. None of these pulse
trains, nor - experiments that take advantage on T1
differences, give - results as good as those that are obtained with
secuences - using gradients, such as WEFT or WATERGATE.
- For the same sample this is what we get with
WEFT