OLAP : Blitzkreig Introduction

1
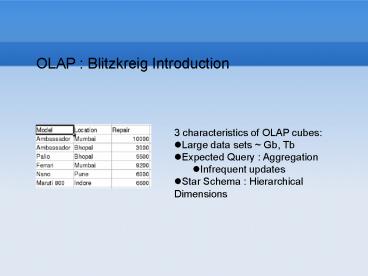
OLAP Blitzkreig Introduction

• 3 characteristics of OLAP cubes
• Large data sets Gb, Tb
• Expected Query Aggregation
• Infrequent updates
• Star Schema Hierarchical Dimensions

2
Attributes and Measures
Attributes are columns with values from a fixed
domain (foreign keys). Measures are numerical
columns.
3
Imprecision and Uncertainity
Imprecision in a tuple refers to an attribute
instantiated by a set of values from the domain
instead of a single value. Uncertainity refers
to a measure represented by a pdf over the domain
instead of a single value.
4
Hierarchical Domains Star Schema
Location
Madhya Pradesh
Maharashtra
Pune
Bhopal
Mumbai
Indore
5
Restriction on Imprecision
We restrict the sets of values in an imprecise
fact to either 1. A singleton set consisting of
a leaf level member of the hierarchy, or, 2. The
set of all the leaf level members under some
non-leaf level member of the hierarchy.
6
Cells and Regions
A region is a vector of attribute values from an
imprecise domains of each dimension of the
cube. A cell is a region in which all values are
leaf level members. Let reg(R) represent the set
of cells in a region R.
7
Queries on precise data
A query Q (R, M, A) refers to a region R, a
measure M, and an aggregate function A. Eg
(ltAmbassador, Locationgt, Repairs, Sum)? The
result of the query in a precise database is
obtained by applying A on the measure M of all
cells in R. For the example above, the result is
(P1 P2)?
8
Queries on imprecise data
Consider the query region ltPune, Modelgt in the
figure. It overlaps two imprecise facts P4 and
P5. Here, we need to make a decision between 3
strategies None Ignore both P4 and P5 because
of their imprecision Contains Take P5 because
it is contained inside the query Overlaps Take
P5, and somehow, P4 as well.
9
Contains option Consistency
Intuitively, consistency means that the answer to
a query should be consistent with the aggregates
from individual partitions of the query. Using
the Contains option could give rise to
inconsistent results. For example, consider the
sum aggregate of the query above and that of its
individual cells. With the Contains option, will
the individual results add up to be the same as
the collective?
10
None option
Essentially, the none option ignores the
imprecise facts, even if a fact is completely
inside the region. Lays waste to the whole
notion of having imprecise facts.
11
Overlaps option Possible Worlds
12
Query semantics on Possible worlds
With each possible world, assign a weight wi such
that the sum of all weights is 1. Intuitively,
the weight of a particular world is like
probability that it is the correct underlying
data. Given a query Q, we can calculate the
result for each vi for each world. Thus, we can
return a pdf over the answer Z as PZ o ? i
v_i o wi A neat short answer could be the
expected value of Z EZ ?i wi vi Problem
with this is number of possible worlds is
exponential in number of imprecise facts!
13
Solution Extended data model
With each cell c in a region r, we add a
probability pr, c, called the allocation of r to
c. The probability of a possible world becomes
the multiple of allocations of ranges to cells
that have been populated in the world. This leads
to a (reasonable) restriction on the kind of
probability distributions on possible worlds.
14
Advantages of EDM

• No extra infrastructure required for representing
  imprecision
• Efficient algorithms for aggregate queries
• SUM and COUNT linear time algo.
• AVERAGE slightly complicated algorithm running
  in O(m n3) for m precise facts and n imprecise
  facts.

15
Allocation Policies
For every region r in the database, we want to
assign an allocation pc, r to each cell c in
Reg(r), such that ?c ? Reg(r) pc, r 1 Three
ways of doing so 1. Uniform Assign each cell
c in a region r an equal probability. pc, r 1
/ Reg(r)
16
Allocation Policies
For every region r in the database, we want to
assign an allocation pc, r to each cell c in
Reg(r), such that ?c ? Reg(r) pc, r 1 However,
we can do better. Some cells may be naturally
inclined to have more probability than others. Eg
Mumbai will clearly have more repairs than
Bhopal. We can do this automatically by giving
more probability to cells with higher number of
precise facts. 2. Count based where
Nc is the number of precise facts in cell c
17
Allocation Policies
For every region r in the database, we want to
assign an allocation pc, r to each cell c in
Reg(r), such that ?c ? Reg(r) pc, r 1 Again,
we can arguably get a better result by looking at
not just the count, but rather than the actual
value of the measure in question. 3. Measure
based next slide.
18
Measure Based Allocation

• Assumes the following model
• The given database D with imprecise facts has
  been generated by randomly injecting imprecision
  in a precise database D'.
• D' assigns value o to a cell c according to some
  unknown pdf P(o, c).
• If we could determine this pdf, the allocation is
  simply
• pc, r P(c) / ? c' in Reg(r) P(c')?

19
Maximum Likelihood Principle
A reasonable estimate for this function P can be
that which maximises the probability of
generating the given imprecise data set
D. Example Suppose the pdf depends only on the
cells and is independent of the measure values.
Thus, the pdf is a mapping ? C ? R where C is
the set of cells. This pdf can be found by
maximising the likelihood function L(?) ?r ?
D ?c ? Reg(r) ?(c)?
20
EM Algorithm
The Expectation Maximization algorithm provides a
standard way of maximizing the likelihood, when
we have some unknown variables in the observation
set. Expectation step (compute data) Calculate
the expected value of the unknown variables,
given the current estimate of variables. Maximizat
ion step (compute generator) Calculate the
distribution that maximizes the probability of
the current estimated data set.
21
EM Algorithm Example
Initialization Step Data 4, 10, ?, ? Initial
mean value 0 New Data 4, 10, 0, 0 Step 1
New Mean 3.5 New Data4, 10, 3.5, 3.5 Step 2
New Mean 5.25 New Data 4, 10, 5.25,
5.25 Step 3 New Mean 6.125 New Data 4, 10,
6.125, 6.125 Result New Mean 6.890625
Step 4 New Mean 6.5625 New Data 4, 10,
6.5625, 6.5625 Step 5 New Mean 6.7825 New
Data 4, 10, 6.7825, 6.7825
22
EM Algorithm Application
23
Experiments Allocation run time
24
Experiments Query run time
25
Experiments Accuracy
26
Summary

• Model for ambiguity Imprecision, Uncertainity
• Querying on uncertain data
• None v/s Contains v/s Overlaps option
• Consistency, Faithfulness
• Possible Worlds interpretation size blowup
• Extended databases allocation
• Aggregation algorithms on Extended databases
• Allocation policies
• Uniform
• Count
• Measure EM algorithm
• Experiments Allocation time, query time,
  accuracy

27
References

• OLAP over uncertain and imprecise data (Doug
  Burdick et al.) - The VLDB Journal (2007)
  16123144
• OLAP over uncertain and imprecise data(Doug
  Burdick et al.) - - The VLDB Journal (2005)?
• http//en.wikipedia.org/wiki/Expectation-maximizat
  ion_algorithm