Number systems, Binary Logic, Gates

1
Number systems, Binary Logic, Gates
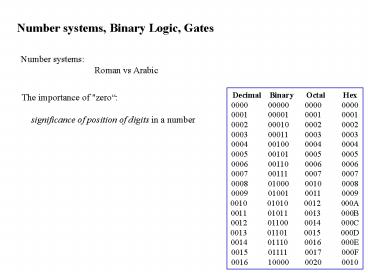
Number systems Roman vs Arabic
Decimal Binary Octal Hex 0000 00000 0000 0000 0001
00001 0001 0001 0002 00010 0002 0002 0003 00011 0
003 0003 0004 00100 0004 0004 0005 00101 0005 0005
0006 00110 0006 0006 0007 00111 0007 0007 0008 01
000 0010 0008 0009 01001 0011 0009 0010 01010 0012
000A 0011 01011 0013 000B 0012 01100 0014 000C 00
13 01101 0015 000D 0014 01110 0016 000E 0015 01111
0017 000F 0016 10000 0020 0010
The importance of "zero significance of
position of digits in a number
2
Number systems
Equivalence of numbers in different systems
Convert 258 to Decimal
Convert 2510 to Octal
3
Coding Binary representation of non-numbers
ASCII
Octal characters 000 NUL001 SOH002 STX003
ETX004 EOT005 ENQ006 ACK007 BEL 010 BS 011
HT 012 NL 013 VT 014 NP 015 CR 016 SO 017
SI 020 DLE021 DC1022 DC2023 DC3024 DC4025
NAK026 SYN027 ETB 030 CAN031 EM 032 SUB033
ESC034 FS 035 GS 036 RS 037 US 040 SP 041
! 042 " 043 044 045 046 047
' 050 ( 051 ) 052 053 054 , 055
- 056 . 057 / 060 0 061 1 062 2 063
3 064 4 065 5 066 6 067 7 070 8 071
9 072 073 074 lt 075 076 gt 077 ?
100 _at_ 101 A 102 B 103 C 104 D 105 E
106 F 107 G 110 H 111 I 112 J 113 K
114 L 115 M 116 N 117 O 120 P 121 Q
122 R 123 S 124 T 125 U 126 V 127 W
130 X 131 Y 132 Z 133 134 \ 135
136 137 _ 140 141 a 142 b 143 c
144 d 145 e 146 f 147 g 150 h 151 i
152 j 153 k 154 l 155 m 156 n 157 o
160 p 161 q 162 r 163 s 164 t 165 u
166 v 167 w 170 x 171 y 172 z 173
174 175 176 177 DEL
Total symbols 128
Total binary digits required ?
Total octal digits required ?
4
Binary Logic and Gates
- We will use electronic circuits to control
logic - We can construct circuits that work
based on presence/absence of voltage - Logic
circuits (complex) are unreliable if multiple
voltage levels have different
interpretations ? We use BINARY LOGIC CIRCUITS
Basis Boolean Algebra
5
Basic operators of Boolean Algebra
AND
OR
NOT
Relation of Boolean Algebra and Discrete Logic
6
Common Logic Gates
7
Truth Tables relation of inputs, output of an
operator
8
Gates basics
Functioning of an NPN transistor
LED
A is ON ? Small current at transistor base
? Collector-Emitter conducts freely ? Current
through LED ? LED is ON
NPN transistor
you will learn these in detail in ELEC xxx
9
Some simple binary number operations
ADDITION
2s COMPLEMENT
- start from the least significant digit - copy
bit-by-bit until (including) the first 1 -
inverted the remaining digits ( 0 ? 1, and
1 ? 0)
Example Binary number, b 0 0 1 0 1 1 0 2's
complement of b 1 1 0 1 0 1 0
10
Binary number operations motivation
Computers have limited representations fixed
length numbers
Consider the following 4-bit additions
borrow
overflow
- how to represent negative numbers? - what does
the borrow mean?
11
Binary number operations motivation..
Conventions - Use of one extra bit, to
identify overflow in addition - Reserve
Most-Significant-Bit (MSB) to identify negative
number - Store ve numbers as 2s complement
of its absolute value
Consequence - MSB is 1 ? -ve number -
replace addition by addition of 2s complement!!
12
Binary number operations motivation...
number (nd) binary (nb) -2's complement ( - n )
3 0 0011 1 1101
5 0 0101 1 1011
7 0 0111 1 1001
8 0 1000 1 1000
CALCULATE 5 - 7 -3 - 3 8 - 3
13
Boolean Algebra
- Developed by George Boole - Wanted to develop a
language-based logic (and or not) - Boolean
Algebra was used by Claude Shannon for design of
logic circuits
- What is algebra ? - Boolean Algebra two
constants 0, 1 variable can take value of any
constant rules to construct expressions rules
to construct statements ( expr1 expr2) logic
for testing truth of a statement
14
Boolean Algebra
constants 1, 0 symbols (, ), ?, ?, ,
variables A, B,
Expressions a series of symbols rules
constant
variable
constant OPb constant
OPu constant
( expression )
( expression ) OPb ( expression )
OPu ( expression )
15
Boolean Algebra
Evaluating an expression - substitute the value
of each variable - use truth table of operators
to evaluate
if X 1, value of expression X ? 1
Statement expression expression
X ? (X ? Y) 1
Truth of a statement if the equality is true
for all possible instantiations of variables
X ? (X ? Y) 1
16
Boolean Algebra
Theorems Statements that are always true.
Some theorems of one variable
17
Boolean Algebra
Some theorems of two variables
de Morgans theorems
18
Boolean Algebra
Use of theorems simplification of expressions
How many gates would we need to implement the
original expression? How many are needed to
implement the equivalent expression?
19
Karnaugh Maps (K-Maps)
Graphical method to simplify expressions
K-Map matrix of 2n elements each
element corresponds to one distinct instantiation
of the variables
20
K-Maps, example
T X ? (X ? Y)
- Write T as a disjunction of eight conjunction
terms (OR of eight AND-terms)
T X ? (X ? Y) X (X ? Y) X X ? XY
- T 1 if any AND-term 1 WHY ? - Put a 1
in each cell corresponding to each AND-term
X X ? XY X ? XY
- Loop all 1s into rectangular BLOCKS
Loop X T
21
K-Maps, example
- T is a disjunction of eight conjunction terms
(OR of eight AND-terms) - T 1 if any AND-term
1 WHY ? - Put a 1 in each cell
corresponding to each AND-term
22
K-Maps, example
How to make loops - Must be rectangular
or square - Must contain 2n cells (1, 2, 4,
8, ) - Must contain no 0 - Can join
leftmost column with rightmost - Can join
top row with bottom - All 1s must belong to
at least one loop - Try to maximize the size
of loops
23
K-Maps construction f cells
Example Elevator control
Elevator is going up Switch A is ON Elevator is
going down Switch B is ON
What about the state AB ?
State that is physically impossible is filled
with f in K-map
f in K-map may be used as 1 or 0
24
K-Maps construction
prime implicant a block which is not entirely
included in a larger block
essential prime implicant a prime implicant with
at least one cell that cannot be included in
any other prime implicant
1. Identify input, output variables formulate
the logic expression 2. Re-write the expression
disjunction of purely conjunctive terms 3. Make
the K-map 4. Fill a 1 in the cell(s)
corresponding to each term, and F where
possible 5. Identify and "block" each essential
prime implicant. 6. If any un-blocked "1" cells
remain, create corresponding prime implicant 7.
Write output disjunction of conjunctive terms
(1 term for each implicant)
25
(No Transcript)