Poisson Distribution

1
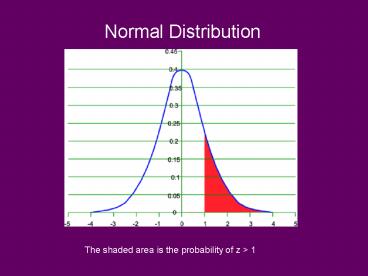
Normal Distribution
The shaded area is the probability of z gt 1
2
The normal distribution is actually a family of
distributions, all with the same shape and
parameterised by mean ?, and standard deviation
?. It is usually defined by a reference member
of the family which is used to define other
members. This reference member has ?0 and ? 1.
3
Definition A random variable Z has a normal (or
Gaussian) distribution with mean 0 and standard
deviation 1, if and only if its distribution
function ?(z) (defined by p(Z ? z) ) is given by
we write Z N(0, 1) and say that Z has a
standard normal distribution
4
Definition A random variable X has a normal (or
Gaussian) distribution with mean ? and standard
deviation ?, if and only if we write X
N(?, ?2) and say that X has a normal distribution
5

6
The normal distribution is symmetric about its
mean ?. In particular, if Z N(0, 1), then
p(Z -z) p(Z
z) i.e. ?(-z) ?(z) 1 for all z
7
Whatever the values of ? and ?, the area between
? - 2? and ? 2? is always 0.95 (95).
8
Similarly, Whatever the values of ? and ?, the
area between ? - ? and ? ? is always 0.68
(68).
9
Example It has been suggested IQ scores follow a
normal distribution with mean 100 and standard
deviation 15. Find the probability that any
person chosen at random will have (a) An IQ
less than 70 (b) An IQ greater than 110 (c) An
IQ between 70 and 110.
10
(No Transcript)
11
In R, The function dnorm gives the density of the
normal distribution. Generally more useful,
though, is pnorm, which gives the cumulative
distribution function.
12
So in the IQ example, the probability of an IQ
less than 70 is
gt pnorm(70,100,15) 1 0.02275013 gt
Approximately 0.0228
13
And the probability of an IQ less than 110 is
gt pnorm(110,100,15) 1 0.7475075 gt

14
Thus, the probability of an IQ more than 110 is 1
- 0.7475075
gt tpnorm(110,100,15) gt 1-t 1 0.2524925 gt

Approximately 0.2525
15
Finally, for the probability of an IQ between 70
and 110, carry out a subtraction.
gt pnorm(110,100,15) - pnorm(70,100,15) 1
0.7247573 gt

Approximately 0.7248
16
Alternatively,
17
gt pnorm(0.6667) - pnorm(-2) 1 0.724768 gt
These are the converted variables in the
standardised normal (z) scales. The answer is, of
course, the same.
18
z -2
z 0.6667
19
The Central Limit

• Theorem

20
Let X1, X2. Xn be independent identically
distributed random variables with mean µ and
variance s 2. Let S X1, X2 . Xn Then
elementary probability theory tells us that E(S)
nµ and var(S) ns 2 . The Central Limit
Theorem (CLT) further states that, provided n is
not too small, S has an approximately normal
distribution with the above mean nµ, and variance
ns 2.
21
In other words, S approx N(nµ, ns 2) The
approximation improves as n increases. We will
use R to demonstrate the CLT.
22
Let X1,X2X6 come from the Uniform distribution,
U(0,1)
1
0
1
23
For any uniform distribution on A,B, µ is equal
to and variance, s2, is equal to
So for our distribution, µ 1/2 and s2 1/12
24
The Central Limit Theorem therefore states that S
should have an approximately normal distribution
with mean nµ (i.e. 6 x 0.5 3) and var ns2
(i.e. 6 x 1/12 0.5) This gives standard
deviation 0.7071 In other words, S approx
N(3, 0.70712)
25
Generate 10 000 results in each of six vectors
for the uniform distribution on 0,1 in R.
gt x1runif(10000) gt x2runif(10000) gt
x3runif(10000) gt x4runif(10000) gt
x5runif(10000) gt x6runif(10000) gt
26
(No Transcript)
27
(No Transcript)
28
Let S X1, X2 . X6
gt sx1x2x3x4x5x6 gt hist(s,nclass20) gt
29
(No Transcript)
30
Consider the mean and standard deviation of S
gt mean(s) 1 3.002503 gt sd(s) 1 0.7070773 gt
This agrees with our earlier calculations
31
A method of examining whether the distribution is
approximately normal is by producing a normal Q-Q
plot. This is a plot of the sorted values of
the vector S (the data) against what is in
effect a idealised sample of the same size from
the N(0,1) distribution.
32
If the CLT holds good, i.e. if S is approximately
normal, then the plot should show an approximate
straight line with intercept equal to the mean of
S (here 3) and slope equal to the standard
deviation of S (here 0.707).
33
gt qqnorm(s) gt
34
From these plots it seems that agreement with the
normal distribution is very good, despite the
fact that we have only taken n 6, i.e. the
convergence is very rapid!
35
Application

• Confidence Intervals for Mean

36
Suppose that the random variables Y1,Y2, Yn
model independent observations from a
distribution with mean µ and variance s2 . Then
is the sample mean.
37
Now by the CLT
This is because µ is replaced by µ/n and s by s
/n (for means)
38
Recall from Statistics 2 that, if s2 is estimated
by the sample variance, s2, an approximate
confidence interval for µ is given by
_
Here y is the observed sample mean, and z is
proportional to the level of confidence required.
39
So for 95 confidence an approximate interval for
µ is given by
2 is approximate - an accurate value can be
obtained from tables or by using the qnorm
function on R.
40
gt qnorm(0.975) 1 1.959964 gt qnorm(0.995) 1
2.575829 gt qnorm(0.025) 1 -1.959964 gt
41
Thus in R, an approximate 95 confidence interval
for the mean µ is given by
gt mean(y)c(-1,1)qnorm(0.975)sqrt(var(y)/length(
y))
where y is the vector of observations. A more
accurate confidence interval, allowing for the
fact that s2 is only an estimate of s2,is given
by use of the function t.test.