Analysis of

1
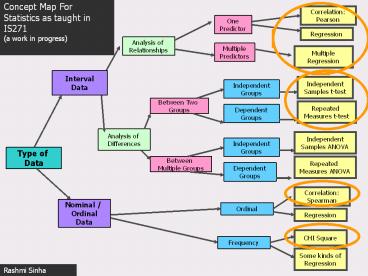
Concept Map For Statistics as taught in IS271 (a
work in progress)
Correlation Pearson
One Predictor
Regression
Analysis of Relationships
Multiple Predictors
Multiple Regression
Interval Data
Independent Samples t-test
Independent Groups
Between Two Groups
Repeated Measures t-test
Dependent Groups
Analysis of Differences
Independent Samples ANOVA
Independent Groups
Type of Data
Between Multiple Groups
Repeated Measures ANOVA
Dependent Groups
Correlation Spearman
Nominal / Ordinal Data
Ordinal
Regression
CHI Square
Frequency
Some kinds of Regression
Rashmi Sinha
2
Analysis of Variance or F test
ANOVA is a technique for using differences
between sample means to draw inferences about the
presence or absence of differences between
populations means.

• The logic of ANOVA and calculation in SPSS
• Magnitude of effect eta squared, omega squared
• Note ANOVA is equivalent to t-test in case of
  two group situation

3
Logic of Analysis of Variance

• Null hypothesis (Ho) Population means from
  different conditions are equal
• m1 m2 m3 m4
• Alternative hypothesis H1
• Not all population means equal.

4
Lets visualize total amount of variance in an
experiment
Total Variance Mean Square Total
Between Group Differences (Mean Square Group)
Error Variance (Individual Differences Random
Variance) Mean Square Error
F ratio is a proportion of the MS group/MS
Error. The larger the group differences, the
bigger the F The larger the error variance, the
smaller the F
5
Logic

• Create a measure of variability among group means
  MSgroup
• Create a measure of variability within groups
  MSerror
• Form ratio of MSgroup /MSerror
• Ratio approximately 1 if null true
• Ratio significantly larger than 1 if null false
• approximately 1 can actually be as high as 2 or
  3, but not much higher
• Look up statistical tables to see if F ratio is
  significant for the specified degrees of freedom

6
Grand mean 3.78
Hypothetical Data
7
Calculations

• Start with Sum of Squares (SS)
• We need
• SStotal
• SSgroups
• SSerror
• Compute degrees of freedom (df )
• Compute mean squares and F

Cont.
8
Calculations--cont.
9
Degrees of Freedom (df )

• Number of observations free to vary
• dftotal N - 1
• N observations
• dfgroups g - 1
• g means
• dferror g (n - 1)
• n observations in each group n - 1 df
• times g groups

10
Summary Table
11
When there are more than two groups

• Significant F only shows that not all groups are
  equal
• We want to know what groups are different.
• Such procedures are designed to control
  familywise error rate.
• Familywise error rate defined
• Contrast with per comparison error rate

12
In case of multiple comparisons Bonferroni
adjustment

• The more tests we run the more likely we are to
  make Type I error.
• Good reason to hold down number of tests
• Run t tests between pairs of groups, as usual
• Hold down number of t tests
• Reject if t exceeds critical value in Bonferroni
  table
• Works by using a more strict level of
  significance for each comparison

13
Bonferroni t--cont.

• Critical value of a for each test set at .05/c,
  where c number of tests run
• Assuming familywise a .05
• e. g. with 3 tests, each t must be significant at
  .05/3 .0167 level.
• With computer printout, just make sure calculated
  probability lt .05/c
• Necessary table is in the book

14
Magnitude of Effect

• Why you need to compute magnitude of effect
  indices
• Eta squared (h2)
• Easy to calculate
• Somewhat biased on the high side
• Percent of variation in the data that can be
  attributed to treatment differences

15
Magnitude of Effect--cont.

• Omega squared (w2)
• Much less biased than h2
• Not as intuitive
• We adjust both numerator and denominator with
  MSerror
• Formula on next slide

16
h2 and w2 for Foa, et al.

• h2 .18 18 of variability in symptoms can be
  accounted for by treatment
• w2 .12 This is a less biased estimate, and
  note that it is 33 smaller.

17
Factorial Analysis of Variance

• What is a factorial design?
• Main effects
• Interactions
• Simple effects
• Magnitude of effect

18
What is a Factorial

• At least two independent variables
• All combinations of each variable
• Rows X Columns factorial
• Cells

2 X 2 Factorial
19
Main effects

• There are two factors in the experiment Source
  of Review and Type of Product.
• If you examine effect of Source of Review
  (ignoring Type of Product for the time being),
  you are looking at the main effect of Source of
  Review.
• If we look at the effect of Type of Product,
  ignoring Source of Review, then you are looking
  at the main effect of Type of Product.

20
Simple effects

• If you could restrict yourself to one level of
  one IV for the time being, and looking at the
  effect of the other IV within that level.
• Effect of Source of Review at one level of
  Product Type (e.g. for one kind of Product), then
  that is a simple effect.
• Effect of Product Type at one level of Source of
  Review (e.g. for one kind of Source, then that is
  a simple effect.

Simple of Effect of Product Type at one level of
Source of Review (I.e., one kind of Review Type,
Expert Review)
21
Interactions (Effect of one variable on the other)
22
Types of Interactions
And this is when there are only two variables!
23
Magnitude of Effect
F ratio is biased because it goes up with sample
size. For a true estimate for the treatment
effect size, use eta squared (the proportion of
the treatment effect / total variance in the
experiment). Eta Squared is a better estimate
than F but it is still a biased estimate. A
better index is Omega Squared.
24
Magnitude of Effect

• Eta Squared
• Interpretation
• Omega squared
• Less biased estimate

k number of levels for the effect in question
25
Omega Squared

26
R2 is also often used. It is based on the sum
of squares. For experiments use Omega Squared.
For correlations use R squared. Value of R
square is greater than omega squared. Cohen
classified effects as Small Effect .01 Medium
Effect .06 Large Effect .15
27
The Data (cell means and standard deviations)
28
Plotting Results
29
Effects to be estimated

• Differences due to instructions
• Errors more in condition without instructions
• Differences due to gender
• Males appear higher than females
• Interaction of video and gender
• What is an interaction?
• Do instructions effect males and females equally?

Cont.
30
Estimated Effects--cont.

• Error
• average within-cell variance
• Sum of squares and mean squares
• Extension of the same concepts in the one-way

31
Calculations

• Total sum of squares
• Main effect sum of squares

Cont.
32
Calculations--cont.

• Interaction sum of squares
• Calculate SScells and subtract SSV and SSG
• SSerror SStotal - SScells
• or, MSerror can be found as average of cell
  variances

33
Degrees of Freedom

• df for main effects number of levels - 1
• df for interaction product of dfmain effects
• df error N - ab N - cells
• dftotal N - 1

34
Calculations for Data

• SStotal requires raw data.
• It is actually 171.50
• SSvideo

Cont.
35
Calculations--cont.

• SSgender

Cont.
36
Calculations--cont.

• SScells
• SSVXG SScells - SSinstruction- SSgender
  171.375 - 105.125 - 66.125 0.125

Cont.
37
Calculations--cont.

• MSerror average of cell variances (4.62
  3.52 4.22 2.82)/4 58.89/4 14.723
• Note that this is MSerror and not SSerror

38
Summary Table
39
Elaborate on Interactions

• Diagrammed on next slide as line graph
• Note parallelism of lines
• Instruction differences did not depend on gender

40
Line Graph of Interaction