An Angular Simple Harmonic Oscillator

1
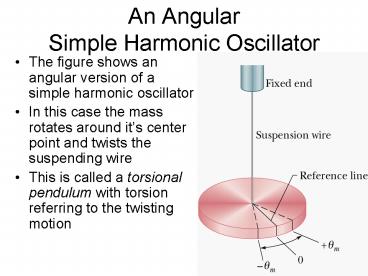
An AngularSimple Harmonic Oscillator

• The figure shows an angular version of a simple
  harmonic oscillator
• In this case the mass rotates around its center
  point and twists the suspending wire
• This is called a torsional pendulum with torsion
  referring to the twisting motion

2
Torsional Oscillator

• If the disk is rotated through an angle (in
  either direction) of ?, the restoring torque is
  given by the equation

3
Pendulums

• When we were discussing the energy in a simple
  harmonic system, we talked about the
  springiness of the system as storing the
  potential energy
• But when we talk about a regular pendulum there
  is nothing springy so where is the potential
  energy stored?

4
The Simple Pendulum

• As we have already seen, the potential energy in
  a simple pendulum is stored in raising the bob up
  against the gravitational force
• The pendulum bob is clearly oscillating as it
  moves back and forth but is it exhibiting SHM?

5

• Going back to our definition of torque, we can
  see that the restoring force is producing a
  torque around the pivot point of

• where L is the moment arm of the applied force

6
The Simple Pendulum
If we substitute t Ia, we get

• This doesnt appear too promising until we make
  the following assumption
• that ? is small
• If ? is small we can use the approximation that
  sin ? ? ?
• (as long as we remember to express ? in radians)

7
The Simple Pendulum

• Making the substitution we then get

which we can then rearrange to get
which is the angular equivalent to
a -? 2 x

• So, we can reasonably say that the motion of a
  pendulum is approximately SHM if the maximum
  angular amplitude is small

8
The Simple Pendulum
The period of a pendulum is given by

• where I is the moment of inertia of the pendulum

• If all of the mass of the pendulum is
  concentrated in the bob, then I mL2 and we
  get

9
The Physical Pendulum

• Now suppose that the mass is not all concentrated
  in the bob?
• In this case the equations are exactly the same,
  but the restoring force acts through the center
  of mass of the body (C in the diagram) which is a
  distance h from the pivot point

10
The Physical Pendulum

• So we go back to our previous equation for the
  period and replace L with h to get

11
The Physical Pendulum

• The other difference in this case is that the
  rotational inertia will not be a simple I mL2
  but rather something more complicated which will
  depend on the shape of the body

12
The Physical Pendulum

• For any physical pendulum that oscillates around
  a point O with period T, there is a simple
  pendulum of length L0 which oscillates with the
  same period
• The point P on the physical pendulum a distance
  L0 from O is called the center of oscillation

13
Measuring g

• The equation for the period of a physical
  pendulum gives us a very nice and neat
  relationship between T, I and g

14

• Suppose we have a uniform rod of length L which
  we allow to rotate from one end as shown
• the moment of inertia I mL2/3
• h L/2

15
Sample Problem 1

• A 1 meter stick swings about a pivot point at one
  end at a distance h from its center of mass
• What is the period of oscillation?

16
Sample Problem 1
17
Sample Problem 2

• What is the distance L0 between the pivot point
  of the stick and the center of oscillation of the
  stick?

18
P 17.15
Value of r for which T is minimum can be obtained
by solving
19
P 17.16
20
P 17.18
21
P 17.11
Momentum conservation gives
22
E 17.32
23
P 17.21
24
P 17.22
25
P 17.19
26
2nd Method
27

• At the right we have a plot of data recorded by
  Galileo of an object (the moon Callisto) that
  moved back and forth relative to the disk of
  Jupiter

28

• The circles are Galileos data points and the
  curve is a best fit to that data
• This would strongly suggest that Callisto
  exhibits SHM

29

• But in fact Callisto is moving with pretty much a
  constant speed in a nearly circular orbit about
  Jupiter
• So what is it that we are seeing in the data?

• What Gallileo saw and what the data tells us
• is that SHM is the projection of uniform
• circular motion in the plane of the motion
• In other words, SHM is uniform circular motion
  viewed edge-on

30

• SHM is the projection of uniform circular motion
  on a diameter of the circle in which the latter
  motion takes place

31
Simple Harmonic Motion Uniform Circular Motion

• We have at the right a reference circle the
  particle at point P is moving on that circle at
  a constant angular speed ?
• The radius of our reference circle is xm
• Finally, the projection of the position of P
  onto the x axis is the point P

32
Simple Harmonic Motion Uniform Circular Motion

• We can easily see that the position of the
  projection point P is given by the formula
• Which is the formula for the displacement of an
  object exhibiting SHM

33
Simple Harmonic Motion Uniform Circular Motion

• Similarly, if we look at the velocity of our
  particle (and use the relationshipv ?r) we can
  see that it obeys

34
Simple Harmonic Motion Uniform Circular Motion

• And finally, if we look at the acceleration of
  our particle (and use the relationship ar ?2r)
  we can see that it obeys

• So regardless of whether we look at displacement,
  velocity or acceleration, we see that the
  projection of uniform circular motion does indeed
  obey the rules of SHM

35
Theory for Problem Nos17.40,17.4117.42
Lissajous figure
Curve which shows the path followed by a particle
having SHM in two perpendicular directions
simultaneously is called Lissajous figure on the
name Mr. J.A.Lissajous(1822-1880)
36
(No Transcript)
37
(No Transcript)
38
(No Transcript)
39
(No Transcript)
40
(No Transcript)
41
(No Transcript)
42
(No Transcript)
43
(No Transcript)
44
(No Transcript)
45
(No Transcript)
46
(No Transcript)
47
Lissajous with irrational frequency ratios
48
(No Transcript)