8'3 Circles

1
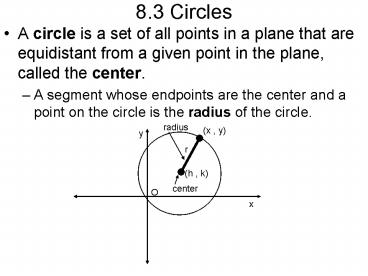
8.3 Circles

• A circle is a set of all points in a plane that
  are equidistant from a given point in the plane,
  called the center.
• A segment whose endpoints are the center and a
  point on the circle is the radius of the circle.

radius
(x , y)
y
r
(h , k)
center
O
x
2
Equation of a Circle

• The equation of a circle with center (h , k) and
  radius r units is
• (x h)2 (y k)2 r2

3
Write an Equation Given the Center and Radius

• Write an equation for the circle that satisfies
  the set of conditions center (-15, 110),
  radius 30 km.
• So, the equation is

4
Write an Equation Given a Diameter

• Write an equation for a circle if the endpoints
  of a diameter are at (5 , 4) and (-2 , -6).
• First find the center of the circle using the
  Midpoint Formula

5
Write an Equation Given a Diameter (Cont.)

• Now find the radius using the distance formula.
• Use the center and the endpoint (5 , 4)

6
Write an Equation Given a Diameter (Cont.)

• Then, substitute h, k, and r2 into the standard
  form of the equation of a circle.

7
Write an Equation Given the Center and a Tangent

• Write an equation for a circle with center at
  (-4 , -3) that is tangent (a line that
  intersects the circle at exactly one point) to
  the x-axis.
• First, sketch the circle. Since the circle is
  tangent to the x-axis, the radius is 3.
• An equation of the circle is (x 4)2 (y 3)2
  9.

(-4 , -3)
8
Graph an Equation in Standard Form

• Find the center and radius of the circle with
  equation x2 y2 25. Then graph the circle.
• The center of the circle is at (0 , 0), and the
  radius is 5.

9
Graph an Equation Not in Standard Form

• Find the center and radius of the circle with
  equation x2 y2 4x 8y 5 0
• Complete the squares.
• Center (2 , -4) Radius 5

10
Graph an Equation Not in Standard Form (Cont.)

• Graph (x 2)2 (y 4)2 25

(2 , -4)
11
More Practice!!!!

• Textbook p. 429 18 24 even, 30 40 even
• Homework Worksheet 8.3