Dijkstra algorithm cont'

1
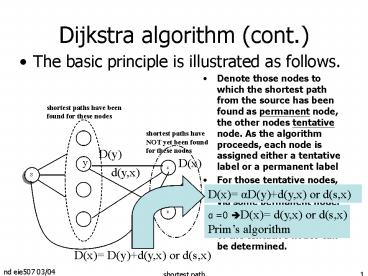
Dijkstra algorithm (cont.)

• The basic principle is illustrated as follows.

• Denote those nodes to which the shortest path
  from the source has been found as permanent node,
  the other nodes tentative node. As the algorithm
  proceeds, each node is assigned either a
  tentative label or a permanent label
• For those tentative nodes, the shortest path must
  be via some permanent node. Based on this
  principle, the shortest path from S to one of the
  tentative nodes can be determined.

shortest paths have been found for these nodes
shortest paths have NOT yet been found for these
nodes
D(y)
D(x)
y
x
d(y,x)
S
z
a 0 ?D(x) d(y,x) or d(s,x) Prims algorithm
D(x) D(y)d(y,x) or d(s,x)
2
Dijkstra algorithm stated

• Dijkstra algorithm can be stated as follows.
• Step 0 The source node s is given a permanent
  label of (0,s) Assign tentative (t) labels (
  D(x)?, u(x) - ) to all nodes other than the
  source node where D(x) is the distance from
  source to this node over the (tentative) shortest
  path and u(x) is the upstream node in the
  shortest path. Let y denote the previous node
  that has been assigned a permanent label set
  ys.
• Step 1 For each tentative node x, redefine d(x)
  as D(x) min D(x), D(y)d(y,x)
• Step 2 Search over all the tentative labels and
  change the label of a node ( D(x), u(x) ) to
  permanent (p) if the D(x) is the smallest among
  all the tentative labels update u(x) as well.
• Step 3 Set yx (update y) If the specific node
  has not yet been given a permanent label, go to
  step 2 otherwise stop (the shortest path from s
  to the specific node has been determined).

3
Prim-Dijkstra a0.5 algorithm an example
3
A
B
2
Steps 2,3 Find p, y
2
4
7
S
T
3
2
3
D
C
Step 1 Update D(x)