Approximating a Function via Pade Approximants

1
State of North Carolina UNDERGRADUATE RESEARCH
CREATIVITY SYMPOSIUM (SNCURCS) UNC WILMINGTON,
November 21, 2009.
Approximating a Function via Pade
Approximants Cardama Pedro1, Mohammad
Siddique1 1Department of Mathematics and Computer
Science, Fayetteville State University,
Fayetteville, North Carolina 28301
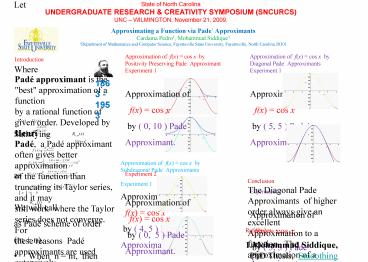
Approximation of f(x) cos x by Diagonal
Pade Approximants Experiment 1 Approximation of
f(x) cos x by ( 5, 5 ) Pade Approximant.
Experiment 2 Approximation of f(x) cos
x by ( 3, 3 ) Pade Approximant.
Approximation of f(x) cos x by Positivity
Preserving Pade Approximant Experiment
1 Approximation of f(x) cos x by ( 0, 10
) Pade Approximant. Experiment
2 Approximation of f(x) cos x by ( 0, 5
) Pade Approximant.
Introduction Padé approximant is the "best"
approximation of a function by a rational
function of given order. Developed by Henri
Padé, a Padé approximant often gives better
approximation of the function than truncating
its Taylor series, and it may still work where
the Taylor series does not converge. For these
reasons Padé approximants are used extensively
in computer calculations.
1863 - 1953

• Pade Approximants
• If and are
  polynomials of degree n and m
• respectively, then is a Padé
  approximation of order
• (m n) to a function and is
  denoted by .
• The Padé approximant to the exponential function
  is
• defined as follows
• Let
• 
  
• 
  
• Where

Approximation of f(x) cos x by Subdiagonal
Pade Approximants Experiment 1 Approximation of
f(x) cos x by ( 4, 5 ) Pade Approximant.
Experiment 2 Approximation of f(x) cos x
by ( 3, 4 ) Pade Approximant.
Conclusion The Diagonal Pade Approximants of
higher order always give an excellent
Approximation to a function. The approximation
of a function by diagonal Pade approximants of
order 10 and Subdiagonal Pade approximant of
order 9 are comparable and give excellent
result. A Positivity Preserving Pade of order
10 Give excellent approximation within a short
interval -1.25, 1.25. The interval of best
approximation for Diagonal Pade and Subdiagonal
Pade are -3, 3 and -2.9, 2.9 respectively.

• References
• Mohammad Siddique, PhD Thesis,  Smoothing with
  positivity-preserving Padé schemes for parabolic
  problems  with nonsmooth data.2002. (Mathematical
  Sciences), QA 10000. S5683x 2002.
• 2. http//www.maplesoft.com/