Charge Density Fluctuations in the presence of spinodal instabilities

1
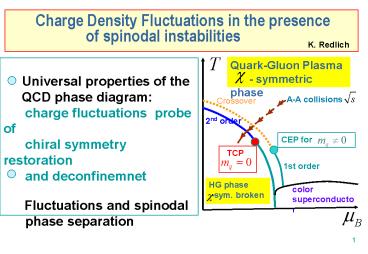
Charge Density Fluctuations in the
presence of spinodal
instabilities


K. Redlich
Quark-Gluon Plasma - symmetric phase
Universal properties of the
QCD phase diagram charge fluctuations
probe of chiral symmetry restoration
and deconfinemnet Fluctuations
and spinodal phase separation

A-A collisions
Crossover
2nd order
CEP for
TCP
1st order
HG phase -sym. broken
color superconductor
2
PNJL model and chiral phase transition

Polyakov loops

• Generic structure of the
• phase diagram as expected in
• QCD and in different chiral models see eg.
  M. Asakawa K. Yazaki J. Berges K. Rajagopal,
  H. Fujii Ohtani M. Harada A. Shibata,
• M. Halasz et al. M. Alford et al,
• A. Hatta T. Ikeda, Ratti, W. Weise
• C. Sasaki, B Schaefer, J. Wambach,..

• Large no CEP at finite T

quantifies repulsive interaction
between quarks
3
Susceptibilities of conserved charges
B. Friman, C. Sasaki K.R.

• Net quark-number ,isovector
• and electric charge
• fluctuations

TCP
1st order
2nd order
No mixing of isospin density with the sigma field
due to isospin conservation
Hatta Stephanov
4
Scaling properties
C.Sasaki, B. Friman K.R.
The strength of the singularity at TCP depends
on direction in plane
Z(2) univer. class
Going beyond the mean field B.-J. Schaefer J.
Wambach
along 1st order line
any direction not parallel
along 2nd order line
Ising
See also Y. Hatta, T. Ikeda
5
Scaling properties
C.Sasaki, B. Friman K.R.
The strength of the singularity at TCP depends
on direction in plane
O(4) univer. class
Z(2) univer. class
Going beyond the mean field B.-J. Schaefer J.
Wambach
along 1st order line
any direction not parallel
along 2nd order line
Ising
See also Y. Hatta, T. Ikeda
6
Quark and isovector fluctuations along critical
line
To find CEP surch for a non-monotonic behavior of
the net quark number susceptibility as a
function of or in heavy ion
collisions as a function of
sensitive probes of CEP
Non-singular behavior at CEP of
7
Ratio of as a probe of
deconfinement
S. Ejiri, F. Karsch, K.R.

• HRG factorization of pressure
• consequently in HRG
• In QGP,
• Ratio of cumulants
• excellent probe of deconfinement

Bulk properties due to flavor content gap of
medium constituents S. Jeon, V. Koch M.
Asakawa, U. Heinz, B. Muller
8
The nature of the 1st order chiral phase
transition
instability of a system
stable
unstable
spinodal
A-B supercooling (symmetric phase) B-C
non-equilibrium state C-D superheating (broken
phase)
9
Phase diagram in the Nambu-Jona-Lasinio model
C.Sasaki, B. Friman K.R.
10
(No Transcript)
11
Net-quark fluctuations on spinodals
CEP
at any spinodal points
spinodals
Singularity at CEP are the remnant of that
along the spinodals
with
12
Experimental Evidence for 1st order transition
Low energy nuclear collisions
Specific heat for constant pressure
13
LGT phase boundary and chemical freezeout

• At present, the critical
• curve and CEP obtained in LGT coincide with
  the chemical freeze-out
• However recent LGT results show that
• there is no unique value
• of at (Y.Aoki at.al)
• Critical temperature at
• can be as large as
• (M. Cheng et al.)

14
Summary

• The net-quark number fluctuations through
  quartic/quadratic cumulants ratio are an
  excellent probe of deconfinement in HIC at the
  LHC
• A non-monotonic change of the net-quark
  susceptibility in
• HIC with the collision energy probes the
  existence of CEP
• However if spinodal phase
• separation occurs then
• Divergence of charge fluctuations appear across
  the 1st order transition along the spinodal lines

Non-equilibrium chiral phase diagram
15
Energy dependent fluctuations CEP
NA49
Smooth change of fluctuations with collision
energy no sign of CEP
16
Compressibility of the QGP
Isothermal compressibility
should be large near CEP
For the HRG gives
Large density fluctuations at saturated by
fluctuations in HRG
Bulk properties due to flavor content gap of
medium constituents S. Jeon, V. Koch M.
Asakawa, U. Heinz, B. Muller
17
Quark fluctuations and O(4) universality class

• Pressure

R. Pisarski, F. Wilczek expected
1st order